Загальні поняття. До цих пір ми розглядали коливальні системи, на які діяли відновлюючі сили, які залежать від узагальнених координат

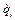До цих пір ми розглядали коливальні системи, на які діяли відновлюючі сили, які залежать від узагальнених координат , дисипативні сили, які залежать від узагальнених швидкостей і змушують сили, що є заданими функціями часу .

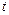Однак існують сили і більш складної природи, які залежать від , .

.

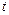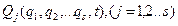таким чином, виділити складові, які залежать тільки від координат і тільки від часу неможливо.

Так, наприклад, у випадку найпростішої лінійної системи рівняння руху можна представити у вигляді

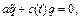(5.1)

де параметр “ 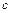” залежить від часу; воно і описує параметричні коливання. Обмежимося лише нагодою періодичної «модуляції» параметра, тобто .

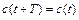Відразу відзначимо, що в залежності від параметрів системи амплітуди параметричних коливань залишаються обмеженими або зростають з часом. Це явище називається параметричним резонансом. Параметричний резонанс має місце при виконанні певних співвідношень між частотою зміни параметра і частотою порушених коливань, близькою або збігається з власною частотою системи, а також при виконанні умов, що стосуються глибини модуляцій параметра.

Наведемо два простих приклади параметричних систем. Для маятника довжиною 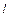, масою вантажу і заданим періодичним законом руху точки підвісу (рис.5.1) диференціальне рівняння щодо руху

Рисунок 5.1– Маятник з точкою підвісу, яка коливається

або

(5.2)

відноситься до типу параметричних (5.1).

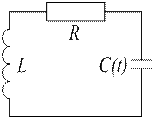
Рисунок 5.2 – Контур зі змінною ємністю

Рисунок 5.3 – Кусково-постійна залежність ємності від часу

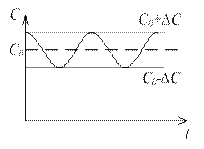
Рисунок 5.4 – Синусоїдальна залежність ємності

В електричному контурі (рис. 5.2) зі змінною ємністю за рахунок якогось зовнішнього пристрою з періодичним кусочно-постійним (рис. 5.3) або синусоїдальним (рис. 5.4) законом можливі при певних умовах як стійкі так і наростаючі коливання.