Параметричне гармонійне обурення

Диференціальне рівняння, відповідне цьому випадку (рис.5.4) запишеться у вигляді

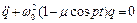, (5.14)

де 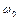- середнє значення власної частоти системи, 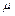– глибина пульсації параметра. Диференціальні рівняння подібного типу називаються рівняннями Матьє. Ними описуються робота параметричного генератора, одноконтурні параметричні підсилювачі, перетворювачі і т.п. Рішеннями рівняння Матьє є спеціальні функції Матьє, або ж застосовується для їх вирішення наближений метод повільно мінливих амплітуд.

Перепишемо рівняння (5.14) у вигляді

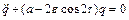, (5.15)

в якому , , .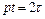

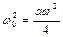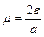Рішення рівняння (5.15) можуть бути обмеженими, а також необмежено зростати. Діаграма стійкості в осях “ 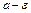” схожа з діаграмою стійкості п.5.2 (рис.5.5).

КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 5

1. Наведіть приклади параметричних систем і поясніть особливості їх рухів.

2. Отримайте приватні рішення диференціальних рівнянь (5.3) в задачі параметричних коливань.

3. Які основні умови досягнення параметричного резонансу?

4. Чому відбудуватися від параметричного резонансу важче, ніж від звичайного?