Зауваження

1. При розрахунку вважають, що розрізані стрижні (на рис. 72 – це стрижні 6, 7, 8) працюють на розтяг, тобто зусилля у цих стрижнях – розтягуючі і зображуються 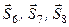, як вказано на рис. 72. Якщо в дійсності який-небудь стрижень стиснутий, то в результаті розрахунку отримаємо від’ємне число для зусилля в ньому.

2. Оскільки розрахунок зусиль в стрижнях ферми в даному способі проводиться за допомогою рівнянь рівноваги плоскої системи сил (а їх є тільки три), то ферму перерізають на дві частини таким чином, щоб в перерізі було не більше трьох стрижнів, зусилля в яких невідомі.

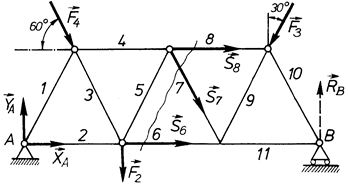
Рис. 72

Питання для самоконтролю

1. Що називається тертям?

2. Що називається тертям ковзання?

3. Що називається тертям кочення?

4. Запишіть формулу, за допомогою якої обчислюється сила тертя ковзання.

5. Що називається кутом тертя?

6. Чому дорівнює тангенс кута тертя?

7. Що таке область рівноваги? Чому вона так називається?

8. Запишіть формулу, за допомогою якої визначається момент тертя кочення.

9. В яких одиницях вимірюються коефіцієнт тертя ковзання і коефіцієнт тертя кочення?

10. Запишіть умову чистого кочення циліндричного тіла по поверхні.

11. Що називається фермою?

12. Як класифікують ферми?

13. Які ферми називаються фермами без зайвих стрижнів?

14. Які ферми називаються статично визначеними?

1.5 Система паралельних сил.
Центр ваги твердого тіла

§ 31 Зведення системи паралельних сил
до канонічного вигляду

Розглянемо систему паралельних сил (рис. 73). Для наочності припустимо, що сили вертикальні, а систему координат виберемо так, що вісь Oz буде паралельна силам. Зведемо задані сили до центра О. Для цього визначимо головний вектор і головний момент відносно точки О заданої системи сил. В нашому випадку маємо

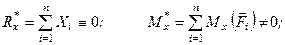
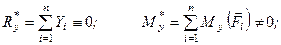
Рис. 73

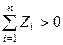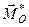З отриманих результатів видно, що в загальному випадку головний вектор і головний момент відносно точки О не дорівнюють нулеві. До того ж головний вектор розглянутої системи сил напрямлений по осі Oz (на рис. 73 головний вектор зображений в припущенні, що ), а головний момент відносно точки О заданої системи сил знаходиться в площині (на рис. 73 вектор зображений в припущенні, що ). Отже, головний вектор і головний момент відносно точки О взаємно перпендикулярні .

Із загальної теорії зведення довільної системи сил до канонічного вигляду відомо, що в даному випадку система сил може бути зрівноваженою (коли 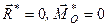), звестись до пари сил (коли ), або — до рівнодійної (коли 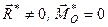або коли і ). Отже, в найбільш загальному випадку система паралельних сил зводиться до рівнодійної.

Для випадку, показаному на рис. 73, рівнодійна паралельна заданій системі сил, лежить в площині перпендикулярній до головного моменту 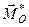і пройде через точку , положення якої знаходиться за формулою (1.45).

Властивість системи паралельних сил характеризується такою теоремою:

при повороті системи паралельних сил навколо їх точок прикладання в один і той самий бік і на один і той самий кут рівнодійна буде повертатися на той самий кут навколо фіксованої точки С, яка називається центром паралельних сил.

Доведення. Нехай система паралельних сил має рівнодійну , відмінну від нуля, і нехай точка С є довільною точкою лінії дії цієї рівнодійної (рис. 74.)

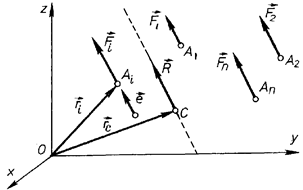
Рис. 74

Нехай: 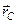– радіус-вектор точки С; – радіус-вектор точки прикладання довільної сили системи; – одиничний вектор напряму дії сил системи. Тоді

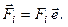(а)

За теоремою Варіньйона маємо

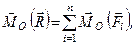
або

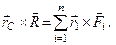(б)

Оскільки 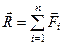і враховуючи (а), отримаємо

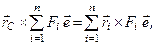
або

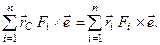
Коли перенесемо всі члени цієї рівності в один бік і винесемо за дужку вектор 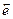, отримаємо

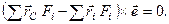(в)

Вимагається, щоб рівність (в) була справедлива для будь-якої орієнтації системи паралельних сил, тобто для будь-якого напряму одиничного вектора . Це можливо, коли

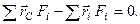(г)

Рівність (г) має єдиний розв’язок відносно радіуса-век-тора 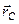, який визначає таку точку прикладання рівнодійної, яка не змінює свого положення при повороті ліній дії сил. Такою точкою і є центр паралельних сил, що і доводить його існування.

Знайдемо радіус-вектор і координати центра паралельних сил. Із (г) маємо

(1.66)

Отримана формула визначає радіус-вектор центра паралельних сил. Спроектувавши обидві частини векторної рівності на координатні осі, отримаємо

(1.67)

Формули (1.67) визначають координати центра паралельних сил.

§ 32 Центр ваги твердого тіла

На всі частинки тіла, що знаходяться поблизу поверхні Землі, діє сила ваги, яка є геометричною сумою сили всесвітнього тяжіння і відцентрової сили інерції, зумовленої обертанням Землі навколо своє осі. Оскільки відцентрова сила інерції мала порівняно із силою тяжіння, то практично вважають, що сила ваги напрямлена до центра Землі. Якщо тіло розбити на елементарні частини, сили ваг яких (рис. 75) і врахувати, що розміри тіла є незначними порівняно з розмірами Землі, то сили ваг їх елементарних частин тіла з достатньо великою точністю утворюють систему паралельних сил.

Рівнодійна сил ваг окремих частин тіла називається
силою ваги тіл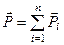а

. (а)

Враховуючи, що сили ваг елементарних частин тіла паралельні і напрямлені в один бік, векторну рівність (а) можна записати у вигляді

(1.68)

тобто

вага тіла дорівнює сумі ваг окремих його частин.

Центр паралельних сил ваг окремих частин тіла називається центром ваги тіла.

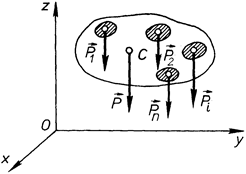
Рис. 75

На рис. 75 центр ваги тіла позначено буквою С. Координати точки С можна обчислити за формулами (1.67), які визначають координати центра паралельних сил, замінивши 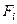на

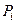
(1.69)

Записані вирази – це найбільш загальні формули, які визначають координати центра ваги тіла. В даних формулах:
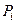– вага окремої частини тіла; – координати цієї частинки.

Сумування в цих формулах проводиться по всіх частинках тіла. Для тіл, вага яких розподілена неперервно по об’єму, сумування замінюють інтегруванням, і формули (1.69) набувають вигляду

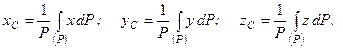(1.70)

Розглянемо деякі часткові випадки.

1. Центр ваги однорідного тіла (центр ваги об’єму)

До однорідних тіл віднесемо тіла, питома вага яких 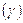по об’єму є сталою, тобто 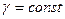. Тоді 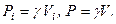Тут 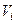– об’єм частинки тіла. 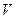– об’єм всього тіла. Підставивши ці значення в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного тіла

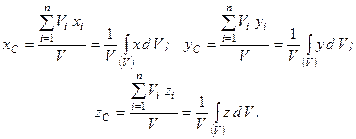(1.71)

Центр ваги однорідного тіла є центром ваги його об’єму.

2. Центр ваги площі однорідного плоского тіла
(центр ваги площі)

Нехай однорідне плоске тіло буде розміщене в площині (рис. 76). Його вага і вага окремої його частини визначаються за формулами

(б)

де: 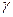– вага одиниці площі тіла; 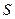– площа тіла; 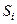– площа елементарної його частини. Підставивши (б) в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного плоского тіла

(1.72)

Рис. 76

Під центром ваги площі (плоскої фігури) розуміють центр ваги тонкої однорідної пластини, основа якої співпадає з даною площею. Координати центра ваги площі визначаються за формулами (1.72).

Зазначимо, що:

сума добутків площі кожного елемента плоскої фігури на його відстань до деякої осі, яка лежить у площині фігури, називається статичним моментом плоскої
фігури відносно цієї осі.

Згідно з цим суми і 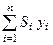є статичні моменти нашої плоскої фігури відносно осей і . Позначаючи ці статичні моменти буквами і 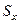, тобто

(1.73)

отримуємо для координат центра ваги плоскої фігури такі формули:

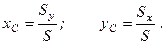(1.74)

За цими формулами вираховують координати центра ваги плоскої фігури, якщо відомі її статичні моменти 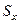і

3. Центр ваги однорідного лінійного тіла
(центр ваги лінії)

Позначимо 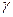– вагу одиниці довжини однорідного лінійного тіла. Тоді його вага і вага його елементарної частини визначається за формулами

(в)

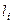де: – довжина тіла; – довжина 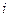-ого елемента. Підставляючи (в) у формули 1.69), отримаємо формули, які визначають координати центра ваги лінійного однорідного тіла (наприклад, дроту, стрижневої конструкції і т.ін.)

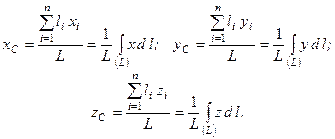(1.75)

Під центром ваги лінії розуміють центр ваги тонкого однорідного тіла (стрижня), середня лінія якого співпадає з даною лінією. Координати центра ваги лінії визначаються за формулами (1.75).

§ 33 Центр ваги деяких простих геометричних фігур

Визначимо центри ваги деяких найпростіших геометричних фігур, які часто зустрічаються в практиці і за допомогою яких можна побудувати більш складні фігури.

Але з самого початку доведемо таку теорему:

якщо тіло має елемент симетрії (площину, вісь, центр симетрії), то центр ваги тіла знаходиться на цьому елементі симетрії.

Дану теорему доведемо для тіла, що має площину симетрії. Припустимо, що тіло А (рис. 77) має площину симетрії 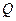. Систему координат виберемо так, щоб координатна площина знаходилась в площині симетрії. Тоді вісь 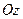буде перпендикулярна до цієї площини. При такому виборі системи координат кожній точці верхньої частини тіла, положення якої визначається координатами ( ), буде відповідати симетрична точка 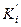нижньої частини тіла з координатами ( ). Якщо навколо даних точок виділити однакові елементарні об’єми , то отримаємо

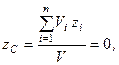(г)

оскільки в сумі всі члени попарно знищуються. Отриманий результат, тобто рівність (г), вказує на те, що центр ваги знаходиться в площині , яка є площиною симетрії тіла.

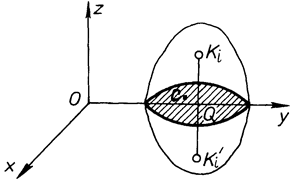
Рис. 77

Аналогічно можна довести, що центр ваги тіла знаходиться на осі симетрії або в центрі симетрії тіла, якщо воно має відповідні елементи симетрії. Доведення цього положення може базуватись на тому, що вісь симетрії – це лінія перетину двох площин симетрії, а центр симетрії – це точка перетину трьох площин симетрії. Якщо центр ваги тіла одночасно знаходиться в двох (трьох) площинах симетрії, то, очевидно, він знаходиться на лінії (точці) перетину цих площин симетрії.

А тепер розглянемо деякі прості геометричні фігури.

Центр ваги площі паралелограма

З курсу математики середньої школи відомо, що точка перетину діагоналей паралелограма є центром його симетрії. Отже, центр ваги паралелограма (прямокутника, ромба) знаходиться в точці перетину його діагоналей.

Центр ваги площі трикутника

Для знаходження центра ваги площі трикутника ABD (рис. 78) розіб’ємо його площу на безліч смужок безконечно малої ширини паралельно до сторони AD. Центр ваги кожної такої смужки буде знаходитись в її центрі, тобто на прямій, що з’єднує вер-шину В трикутника з сере-диною протилежної сторо-ни, а це є медіана ВК трикутника. Звідси робимо висновок, що й центр ваги площі всього трикутника лежить на цій медіані.

Розбиваючи трикутник на елементарні смужки лініями, що паралельні стороні АВ (рис. 78), отримаємо, що центр ваги площі трикутника буде знаходитись на медіані DM.

Отже,

центр ваги площі трикутника знаходиться в точці перетину його медіан.

В аналітичній геометрії доводиться, що координати точки перетину медіан трикутника визначаються за формулами

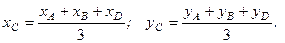(1.76)

Формули (1.76) визначають координати центра ваги трикутника. В цих формулах 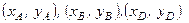– координати вершин трикутника.