Складний рух точки

Складним рухом точки називається такий її рух, при якому точка одночасно рухається відносно двох або більше систем відліку, одна з яких нерухома.

Так, наприклад, переміщення пасажира в рухомому поїзді відносно Землі є складним рухом. По-перше, пасажир рухається з поїздом, по-друге, пасажир переміщується відносно вагона (поїзда). Якщо врахувати рух Землі, то всі тіла, які рухаються по поверхні Землі, здійснюють також складний рух, адже вони рухаються разом з Землею і переміщаються відносно її поверхні. Прикладів складного руху точки можна навести безліч, бо рух кожного тіла (точки), якщо дивитись “в корінь”, є складним.

Вивчення складного руху є важливим не тільки тому, що всі тіла (точки) фактично його здійснюють, а й тому, що розв’язання багатьох задач на кінематичний розрахунок ефективно проводити шляхом розкладання заданого руху на більш прості рухи. До того ж розв’язання великої кількості задач механіки (наприклад, розрахунок траєкторії польоту космічних апаратів; розробка теорії навігаційних приладів і т.п.) потребує врахування руху систем відліку.

§ 44.1 Основні поняття і визначення

Складний рух точки будемо вивчати на моделі, яка зображена на рис. 107, де позначено:

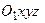– нерухому систему координат;

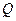– тіло, яке здійснює деякий рух в системі координат 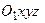; в подальшому це тіло будемо називати носієм;

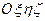– рухому систему координат, яка жорстко зв’язана з носієм;

– точка, яка рухається по носію;

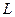– траєкторія руху точки по носію;

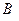– точка носія, з якою в даний момент співпадає рухома точка;

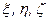– координати точки в рухомій системі координат.

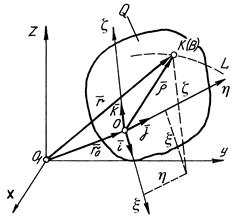
Рис. 107

Рух точки відносно системи координат 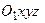є складним. Він складається з руху точки відносно носія і руху, який надається точці носієм.

Введемо основні поняття і визначення, якими користуються при розгляді складного руху точки.

1. Рух точки К відносно нерухомої системи координат називається абсолютним рухом. Траєкторія, швидкість і пришвидшення точки в абсолютному русі, тобто відносно нерухомої системи координат 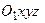, називаються абсолютними.

Абсолютну швидкість і абсолютне пришвидшення позначають відповідно 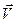і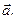

Згідно з рис. 107 положення точки в нерухомій системі координат визначається радіусом-вектором 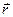, тоді рівняння

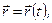
очевидно, описуватиме абсолютний рух точки. Абсолютна швидкість і пришвидшення визначається як відповідні похідні за часом від радіуса-вектор 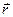, тобто

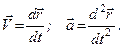(a)

2. Рух точки К відносно рухомої системи координат називається відносним рухом. Траєкторія, швидкість і пришвидшення точки у відносному русі, тобто відносно рухомої системи координат 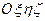(носія), називаються відносними.

Відносна швидкість і відносне пришвидшення позначаються відповідно 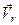і 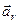(індекс “ 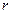” від французького слова relatif – відносний).

Положення точки в рухомій системі координат визначається радіусом-вектором 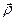, зміна якого зумовлена двома причинами: відносним рухом точки; переміщенням рухомої системи координат. Щоб виключити останню причину зміни 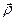, необхідно рухому систему координат умовно зупинити (“заморозити”). Замороження рухомої системи координат
математично позначається 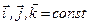. За такої умови 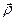як функція часу буде описувати відносний рух точки, тобто рівняння

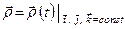
описує відносний рух точки. Відносна швидкість і пришвидшення визначаються як відповідні похідні за часом від радіуса-вектора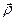

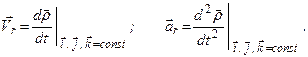(б)

3. Рух рухомої системи координат (носія) відносно нерухомої системи координат називається переносним рухом. Швидкість і пришвидшення точки носія, з якою в даний момент співпадає точка , називається переносними.

Переносна швидкість і переносне пришвидшення позначається відповідно і 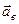(індекс “ 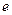” від французького слова entrainer – переносити). В нашому випадку точка , яка здійснює складний рух, в даний момент часу співпадає з точкою носія (рис. 107), отже швидкість і пришвидшення точки для точки будуть переносними, тобто:

(в)

Як приклад, розглянемо переміщення пасажира в рухомому поїзді. Як було сказано вище, пасажир здійснює складний рух – рухається разом з поїздом і переміщається відносно поїзда (вагона). То згідно зі сформульованими визначеннями рух пасажира відносно поверхні Землі (в даному прикладі Землю вважаємо нерухомою) буде абсолютним рухом. Швидкість і пришвидшення пасажира відносно поверхні Землі є абсолютними. Переміщення пасажира відносно поїзда (вагона) є відносним рухом. Швидкість і пришвидшення пасажира відносно вагона є відносними. Для встановлення відносного руху пасажира і його характеристик необхідно, щоб спостерігач перебував у цьому ж вагоні, а це означає, що носій (в нашому випадку вагон) відносно спостерігача “заморожений”. Рух вагона для пасажира буде переносним рухом. І дійсно, вагон переносить пасажира відносно поверхні Землі. Переносною швидкістю і переносним пришвидшенням для пасажира будуть швидкість і пришвидшення точки вагона, з якою в даний момент співпадає пасажир. Враховуючи, що вагон здійснює поступальний рух, швидкість і пришвидшення вагона для пасажира будуть переносними.

Основним завданням теоретичного курсу кінематики складного руху точки є встановлення залежності між кінематичними характеристиками абсолютного, переносного і відносного рухів.