Теорема Ейлера-Даламбера
Як видно з попереднього, обертання тіла навколо нерухомої точки складається з обертань трьох осей 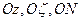 . Виходячи з цього, можна отримати відповідні формули для визначення кінематичних характеристик руху тіла і його точок. Отримати дані формули можна і іншим шляхом. Для цього розглянемо теорему Ейлера-Даламбера:
. Виходячи з цього, можна отримати відповідні формули для визначення кінематичних характеристик руху тіла і його точок. Отримати дані формули можна і іншим шляхом. Для цього розглянемо теорему Ейлера-Даламбера:
усяке переміщення твердого тіла, що має одну нерухому точку, можна здійснити шляхом одного повороту навколо деякої осі, що проходить через нерухому точку.

 Для доведення даної теореми зауважимо, що положення твердого тіла в просторі однозначно визначається положенням трьох його точок, які не лежать на одній прямій. І дійсно (рис. 135), положення двох точок А і В тіла визначає положення деякої осі тіла Аz, а положення третьої точки С – кут повороту тіла відносно даної осі. До того ж при закріпленні даних точок тіло стане нерухомим, тобто займе деяке конкретне положення, що є ще одним підтверд-женням, що положення тіла в просторі цілком визначається положенням трьох його точок.
Для доведення даної теореми зауважимо, що положення твердого тіла в просторі однозначно визначається положенням трьох його точок, які не лежать на одній прямій. І дійсно (рис. 135), положення двох точок А і В тіла визначає положення деякої осі тіла Аz, а положення третьої точки С – кут повороту тіла відносно даної осі. До того ж при закріпленні даних точок тіло стане нерухомим, тобто займе деяке конкретне положення, що є ще одним підтверд-женням, що положення тіла в просторі цілком визначається положенням трьох його точок.
Перейдемо тепер до доведення сформульованої вище теореми. Для цього розглянемо деяке тверде тіло, яке обертається навколо нерухомої точки О (рис. 136). Положення тіла будемо визначати положенням трьох його точок: О – нерухома точка; А і В – дві довільні точки тіла, що знаходяться від нерухомої точки на однаковій відстані (ОА=ОВ), але не лежить з нею на одній прямій. Проведемо через ці точки сферу з центром в точці О.
Через точки А і В проведемо дугу 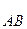 великого кола (дуга великого кола – це дуга кола, центр якого знаходиться в нерухомій точці О). Оскільки точка О нерухома, то положення тіла буде визначатись положенням дуги
великого кола (дуга великого кола – це дуга кола, центр якого знаходиться в нерухомій точці О). Оскільки точка О нерухома, то положення тіла буде визначатись положенням дуги 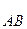 .
.
Припустимо, що в момент часу 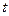 тіло займає положення
тіло займає положення 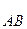 , а в момент часу
, а в момент часу 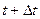 – положення
– положення 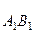 , тобто за деякий проміжок часу
, тобто за деякий проміжок часу 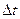 тіло перемістилось з положення
тіло перемістилось з положення 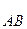 в положення
в положення 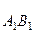 . Проведемо дуги
. Проведемо дуги 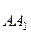 і
і 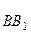 великих кіл.
великих кіл.
Через точки Е і К, які ділять відповідно 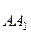 і
і 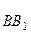 навпіл, проведемо перпендикулярно до даних дуг дуги великих кіл. Позначимо Н точку перетину щойно проведених дуг і з’єднаємо її дугами великих кіл з точками А, В, А1, В1. Отримаємо (на рис. 136 вони заштриховані) сферичні трикутники АВН і А1В1Н, які є рівними за рівністю трьох сторін:
навпіл, проведемо перпендикулярно до даних дуг дуги великих кіл. Позначимо Н точку перетину щойно проведених дуг і з’єднаємо її дугами великих кіл з точками А, В, А1, В1. Отримаємо (на рис. 136 вони заштриховані) сферичні трикутники АВН і А1В1Н, які є рівними за рівністю трьох сторін:
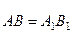 , бо в твердому тілі відстані між точками зберігаються;
, бо в твердому тілі відстані між точками зберігаються;
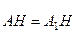 – це випливає з рівності сферичних прямокутних трикутників АЕН і А1ЕН, в яких сторона ЕН є спільною
– це випливає з рівності сферичних прямокутних трикутників АЕН і А1ЕН, в яких сторона ЕН є спільною 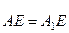 – за побудовою;
– за побудовою;
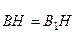 – це випливає з рівності сферичних прямокутних трикутників ВКН і В1КН, в яких сторона КН є спільною, а
– це випливає з рівності сферичних прямокутних трикутників ВКН і В1КН, в яких сторона КН є спільною, а 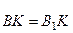 – за побудовою.
– за побудовою.
В рівних трикутниках відповідні кути є рівними, отже
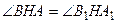 .
.
Додаючи до обох частин цієї рівності по куту 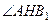 , отримаємо
, отримаємо
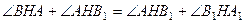
або
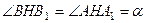 .
.
Отже, при переміщенні тіла з положення АВ в положення 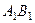 для суміщення точок
для суміщення точок  з
з 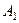 і
і  з
з 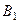 достатньо здійснити обертальний рух на один і той же кут
достатньо здійснити обертальний рух на один і той же кут  , а це означає, що все тіло як одне ціле повернуте на той же кут
, а це означає, що все тіло як одне ціле повернуте на той же кут  . При такому повороті залишаються нерухомими дві точки: точка О і точка Н. Вісь
. При такому повороті залишаються нерухомими дві точки: точка О і точка Н. Вісь 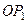 , яка проходить через ці точки, також буде нерухомою. Таким чином, переміщення тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі
, яка проходить через ці точки, також буде нерухомою. Таким чином, переміщення тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі 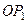 на кут
на кут  . Вісь
. Вісь 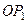 називається віссю кінцевого повороту, а кут
називається віссю кінцевого повороту, а кут  – кутом кінцевого повороту.
– кутом кінцевого повороту.
Якщо усяке переміщення твердого тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі кінцевого повороту, то, очевидно, і нескінченно мале його переміщення також може бути здійснене таким чином. При наближенні нескінченно малого переміщення до нуля положення тіла наближається до його першого положення. Разом з тим вісь 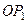 наближається до деякого граничного положення
наближається до деякого граничного положення 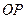 , яке називається миттєвою віссю обертання для заданого моменту часу.
, яке називається миттєвою віссю обертання для заданого моменту часу.
Отже, в кожний момент часу 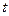 обертання твердого тіла навколо нерухомої точки можна розглядати як обертання навколо миттєвої осі, яка проходить через нерухому точку.
обертання твердого тіла навколо нерухомої точки можна розглядати як обертання навколо миттєвої осі, яка проходить через нерухому точку.
Для кожного моменту часу миттєва вісь обертання займає своє положення, і з часом описує конічну поверхню.
Конічна поверхня, яка описується миттєвою віссю обертання в нерухомому просторі (в просторі системи координат Оxyz), називається нерухомим аксоїдом.
Конічна поверхня, яка описується миттєвою віссю обертання в рухомому просторі (в просторі системи координат Oxhz ), називається рухомим аксоїдом.
При обертанні тіла навколо нерухомої точки рухомий аксоїд, змінюючи своє положення, рухається по поверхні нерухомого аксоїда.
§ 47.3 Кутова швидкість і кутове пришвидшення тіла,
що обертається навколо нерухомої точки
Оскільки обертання тіла навколо нерухомої точки в кожний момент часу можна вважати обертанням навколо миттєвої осі, то
кутова швидкість, з якою в кожний момент часу тіло, що має нерухому точку, обертається навколо миттєвої осі, називається кутовою швидкістю тіла в даний момент часу.
 Вектор кутової швидкості
Вектор кутової швидкості  відкладається з нерухомої точки вздовж миттєвої осі обертання в той бік, звідки обертання тіла видно проти руху годинникової стрілки (рис. 137).
відкладається з нерухомої точки вздовж миттєвої осі обертання в той бік, звідки обертання тіла видно проти руху годинникової стрілки (рис. 137).
Оскільки при русі точки навколо нерухомої точки не існує такого кута як функції часу, похідна від якого дорівнювала б кутовій швидкості, то кутова швидкість повинна бути задана як функція часу або вона може бути представлена через кути Ейлера і їх похідні.
Як було показано в § 47.1, при русі тіла з однією закріпленою точкою воно одночасно обертається навколо трьох осей, що перетинаються (рис. 138), з кутовими швидкостями 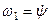 ;
; 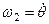 і
і 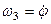 .
.
При такому русі тіла, як буде показано в § 49.3, формула (2.103), вектор результуючої миттєвої кутової швидкості дорівнює
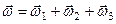 . (а)
. (а)
Для знаходження величини і напряму вектора кутової швидкості  визначимо його проекції на осі рухомої системи координат
визначимо його проекції на осі рухомої системи координат 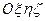 .
.
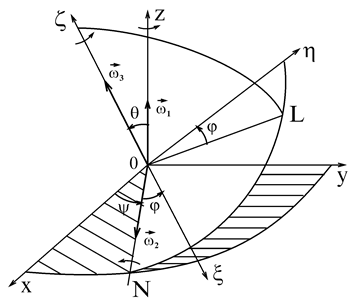
Рис. 138
Проектуючи обидві частини рівності (а) на осі 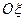 ,
, 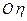 ,
, 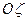 , отримаємо
, отримаємо
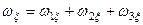 ;
;
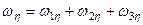 ; (б)
; (б)
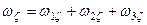 .
.
Проекції векторів 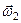 і
і 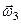 знаходяться безпосереднім проектуванням (рис. 138)
знаходяться безпосереднім проектуванням (рис. 138)
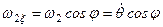 ;
; 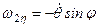 ;
; 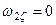 ;
;
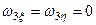 ;
; 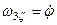 ,
,
а для знаходження проекції вектора 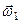 проведемо через осі
проведемо через осі 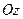 і
і 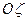 площину, яка перетнеться з площиною
площину, яка перетнеться з площиною 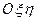 вздовж лінії
вздовж лінії 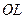 . Оскільки лінія вузлів
. Оскільки лінія вузлів 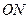 перпендикулярна до площини
перпендикулярна до площини 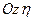 , то вона перпендикулярна і до лінії
, то вона перпендикулярна і до лінії 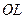 , а
, а 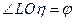 . Тоді, проектуючи вектор
. Тоді, проектуючи вектор 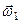 на площину
на площину 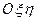 (проекція лежатиме на лінії
(проекція лежатиме на лінії 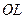 ), а одержану проекцію, в свою чергу, на осі
), а одержану проекцію, в свою чергу, на осі 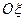 і
і 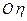 , отримаємо
, отримаємо
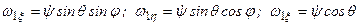 .
.
Підставляючи одержані проекції в праві частини рівностей (б), отримаємо
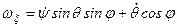 ;
;
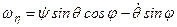 ; (2.78)
; (2.78)
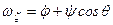 .
.
Аналогічно проектуючи рівність (а) на осі нерухомої системи координат 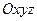 , знайдемо проекції вектора
, знайдемо проекції вектора  на ці осі
на ці осі
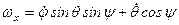 ;
;
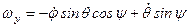 ; (2.78 а)
; (2.78 а)
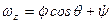 .
.
Рівності (2.78) і (2.78 а) називаються кінематичними рівняннями Ейлера. Вони дають можливість знайти модуль миттєвої кутової швидкості і напрямні косинуси вектора  з відповідними осями координат
з відповідними осями координат
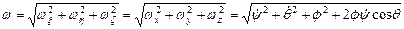 ;
;



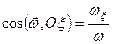 ;
; 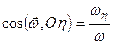 ;
; 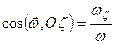 ;
;



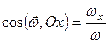 ;
; 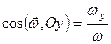 ;
; 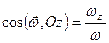 .
.
Перша похідна за часом від вектора кутової швидкості називається вектором кутового пришвидшення
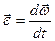 . (2.79)
. (2.79)
 Вектор кутового пришвидшення
Вектор кутового пришвидшення 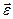 також відкладають з нерухомої точки
також відкладають з нерухомої точки  , навколо якої обертається тіло, але цей вектор (на відміну від обертання тіла навколо нерухомої осі) не буде напрямлений вздовж миттєвої осі обертання, бо кутова швидкість тіла, яке обертається навколо нерухомої точки, може змінюватись як за величиною, так і за напрямом.
, навколо якої обертається тіло, але цей вектор (на відміну від обертання тіла навколо нерухомої осі) не буде напрямлений вздовж миттєвої осі обертання, бо кутова швидкість тіла, яке обертається навколо нерухомої точки, може змінюватись як за величиною, так і за напрямом.
Напрям і величину вектора кутового пришвидшення 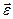 можна знайти таким способом. Позначимо (рис. 139) кінець вектора кутової швидкості
можна знайти таким способом. Позначимо (рис. 139) кінець вектора кутової швидкості  буквою К. Оскільки вектор
буквою К. Оскільки вектор  з часом змінює свою величину і напрям, то точка
з часом змінює свою величину і напрям, то точка  переміщається з часом у просторі, описуючи деяку криву
переміщається з часом у просторі, описуючи деяку криву 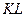 (рис. 139), яка називається годографом век-тора кутової швидкості.
(рис. 139), яка називається годографом век-тора кутової швидкості.
Вектор  визначає положення точки
визначає положення точки  в просторі, отже для даної точки він є радіусом-вектором, а це означає, що
в просторі, отже для даної точки він є радіусом-вектором, а це означає, що
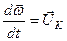 , (в)
, (в)
де 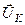 – вектор швидкості точки
– вектор швидкості точки  , який, як відомо, напрямлений вздовж дотичної до траєкторії руху точки.
, який, як відомо, напрямлений вздовж дотичної до траєкторії руху точки.
Порівнюючи (2.79) і (в), робимо висновок, що
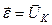 , (2.80)
, (2.80)
тобто:
вектор кутового пришвидшення тіла, котре обертається навколо нерухомої точки, геометрично до-рівнює вектору швидкості точки, яка описує годо-граф вектора кутової швидкості.
Отже, вектор кутового пришвидшення 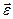 , який, як було сказано вище, відкладається з нерухомої точки, є паралельним вектору
, який, як було сказано вище, відкладається з нерухомої точки, є паралельним вектору 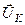 , котрий напрямлений вздовж дотичної до годографа вектора кутової швидкості (рис. 139). Рівність (2.80) часто використовують для визначення кутового пришвидшення тіла, яке обертається навколо нерухомої точки. Для цього, використовуючи відомі способи, визначають величину і напрям вектора швидкості, який описує годограф вектора кутової швидкості. Величина і напрям вектора
, котрий напрямлений вздовж дотичної до годографа вектора кутової швидкості (рис. 139). Рівність (2.80) часто використовують для визначення кутового пришвидшення тіла, яке обертається навколо нерухомої точки. Для цього, використовуючи відомі способи, визначають величину і напрям вектора швидкості, який описує годограф вектора кутової швидкості. Величина і напрям вектора 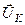 визначає величину і напрям вектора
визначає величину і напрям вектора 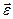 .
.
Пряму 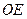 (рис. 139), вздовж якої напрямлений вектор
(рис. 139), вздовж якої напрямлений вектор 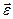 , можна назвати миттєвою лінією кутового пришвидшення.
, можна назвати миттєвою лінією кутового пришвидшення.
Величину і напрям кутового пришвидшення можна також знайти аналітично за допомогою формул
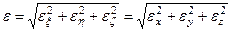 ;
;


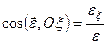 ;
; 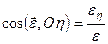 ;
; 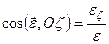 ;
;




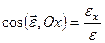 ;
; 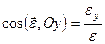 ;
; 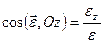 ,
,
де 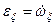 ;
; 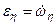 ;
; 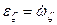 ;
; 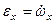 ;
; 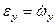 ;
; 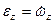 .
.
§ 47.4 Швидкість точок твердого тіла,
яке обертається навколо нерухомої точки
Оскільки обертання твердого тіла навколо нерухомої точки в кожний момент часу можна розглядати як обертання навколо миттєвої осі, то швидкість будь-якої точки  тіла в кожний момент часу можна визначити за формулою Ейлера (2.53)
тіла в кожний момент часу можна визначити за формулою Ейлера (2.53)
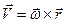 , (а)
, (а)
в якій:  – вектор кутової швидкості тіла;
– вектор кутової швидкості тіла; 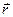 – радіус-вектор точки, швидкість якої визначається. Його можна проводити, як у випадку обертання навколо нерухомої осі, з будь-якої точки миттєвої осі. Але найвигідніше його провести з нерухомої точки тіла, як вказано на рис. 140.
– радіус-вектор точки, швидкість якої визначається. Його можна проводити, як у випадку обертання навколо нерухомої осі, з будь-якої точки миттєвої осі. Але найвигідніше його провести з нерухомої точки тіла, як вказано на рис. 140.
 З визначення векторного добутку безпосередньо випливає:
З визначення векторного добутку безпосередньо випливає:
1. Вектор швидкості точки тіла, яке обертається навколо нерухомої точки, перпендикулярний до площини, в якій знаходяться вектори  і
і 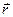 і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора до другого, щоб їх сумістити, видно проти руху годинникової стрілки.
і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора до другого, щоб їх сумістити, видно проти руху годинникової стрілки.
2. Величина швидкості 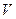 дорівнює
дорівнює

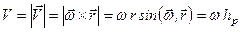 ,
,
тобто
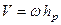 . (2.81)
. (2.81)
Швидкість точки тіла, яке обертається навколо нерухомої точки, чисельно дорівнює добутку кутової швидкості тіла на відстань даної точки до миттєвої осі обертання.
Формулу (2.81) використовують не тільки для визначення швидкості точки тіла, яке здійснює сферичний рух. Її часто використовують і для визначення кутової швидкості самого тіла. Для цього шукають точку, швидкість якої можна визначити, не застосовуючи формулу (2.81). Знайдену швидкість ділять на відстань даної точки до миттєвої осі обертання, положення якої часто визначають з механічної умови задачі і отримують кутову швидкість тіла.
Якщо нерухому точку  вибрати за початок нерухомої і рухомої систем координат (див. рис. 133) і координати точки, швидкість якої визначається, позначити відповідно через (
вибрати за початок нерухомої і рухомої систем координат (див. рис. 133) і координати точки, швидкість якої визначається, позначити відповідно через ( 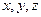 ) – в нерухомій системі координат, (
) – в нерухомій системі координат, ( 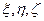 ) – в рухомій, то на основі формул для проекцій векторного добутку на координатні осі з формули (а) отримаємо
) – в рухомій, то на основі формул для проекцій векторного добутку на координатні осі з формули (а) отримаємо
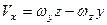 ;
;
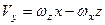 ; (2.82)
; (2.82)
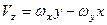 ;
;
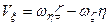 ;
;
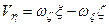 ; (2.83)
; (2.83)
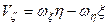 .
.
Формули (2.82) визначають проекції вектора швидкості точки тіла, яке здійснює сферичний рух, на нерухомі осі координат, а формули (2.83) – проекції на рухомі осі координат. В даних формулах 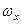 ,
, 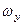 ,
, 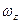 ,
, 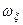 ,
, 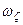 ,
, 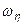 – проекції вектора кутової швидкості на відповідні осі координат.
– проекції вектора кутової швидкості на відповідні осі координат.
Якщо точка знаходиться на миттєвій осі обертання, то швидкість її дорівнює нулеві ( 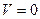 ), а це означає, що дорівнюють нулеві проекції вектора швидкості на координатні осі. З формул (2.82) отримаємо рівняння миттєвої осі обертання в нерухомій системі координат
), а це означає, що дорівнюють нулеві проекції вектора швидкості на координатні осі. З формул (2.82) отримаємо рівняння миттєвої осі обертання в нерухомій системі координат
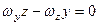 ;
;
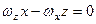 ;
;
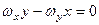 ,
,
або
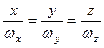 . (2.84)
. (2.84)
Отримане рівняння для конкретного моменту часу є рівнянням миттєвої осі обертання в нерухомій системі координат.
Якщо величини, які входять в рівняння (2.84), розглядати як функцію часу, то дане рівняння є параметричним рівнянням нерухомого аксоїда. Аналогічно з формул (2.83) можна отримати параметричне рівняння рухомого аксоїда
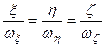 . (2.85)
. (2.85)
§ 47.5 Пришвидшення точок твердого тіла,
яке обертається навколо нерухомої точки
Розглянемо тверде тіло, яке обертається навколо нерухомої точки  , і візьмемо в ньому яку-небудь точку
, і візьмемо в ньому яку-небудь точку  (рис. 141). На цьому ж рисунку зображено:
(рис. 141). На цьому ж рисунку зображено:
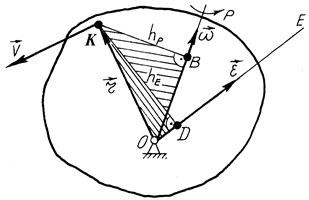
Рис. 141
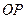 – миттєву вісь обертання;
– миттєву вісь обертання;
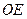 – миттєву лінію кутового пришвидшення;
– миттєву лінію кутового пришвидшення;
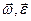 – вектори відповідно кутової швидкості і кутового пришвидшення тіла в деякий момент часу;
– вектори відповідно кутової швидкості і кутового пришвидшення тіла в деякий момент часу;
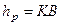 – відстань точки
– відстань точки  до миттєвої осі обертання;
до миттєвої осі обертання;
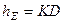 – відстань даної точки до лінії кутового пришвидшення;
– відстань даної точки до лінії кутового пришвидшення;
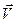 – вектор швидкості точки
– вектор швидкості точки  , який згідно з попереднім визначається за формулою
, який згідно з попереднім визначається за формулою
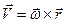 .
.
За визначенням пришвидшення (пришвидшення – це перша похідна за часом від вектора швидкості) і, враховуючи правило диференціювання векторного добутку, матимемо
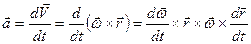 .
.
Враховуючи, що 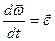 , а
, а 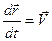 , отримаємо
, отримаємо
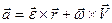 . (а)
. (а)
Таким чином, шукане пришвидшення складається з двох доданків. Знайдемо величину і напрями цих доданків і введемо відповідні позначення.
Векторний добуток 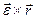 називається обертальним пришвидшенням і позначається
називається обертальним пришвидшенням і позначається 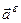 . Отже,
. Отже,
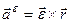 . (2.86)
. (2.86)
Його величина, згідно з правилами обчислення векторного добутку, дорівнює


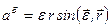 .
.
З 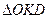 (рис. 141) маємо
(рис. 141) маємо 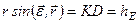 .
.
Отже
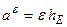 . (2.87)
. (2.87)
Обертальне пришвидшення точки тіла, яке рухається навколо нерухомої точки, чисельно дорівнює добутку кутового пришвидшення тіла на відстань даної точки до лінії кутового пришвидшення.
Вектор обертального пришвидшення 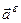 за визначенням векторного добутку перпендикулярний до площини, яка проходить через вектори
за визначенням векторного добутку перпендикулярний до площини, яка проходить через вектори 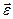 і
і 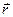 , або, що те саме, – до площини, яка проходить через вектор кутового пришвидшення
, або, що те саме, – до площини, яка проходить через вектор кутового пришвидшення 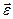 і точку
і точку  (див. рис. 141) і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора
(див. рис. 141) і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора 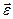 до другого –
до другого – 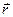 , щоб їх сумістити, видно проти руху годинникової стрілки.
, щоб їх сумістити, видно проти руху годинникової стрілки.
Треба зазначити, що в даному випадку обертальне пришвидшення 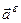 не можна називати дотичним, бо воно загалом не співпадає з напрямом вектора швидкості
не можна називати дотичним, бо воно загалом не співпадає з напрямом вектора швидкості 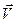 . І дійсно, швид-кість
. І дійсно, швид-кість 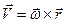 напрямлена перпендикулярно до площини, яка утворена векторами
напрямлена перпендикулярно до площини, яка утворена векторами  і
і 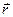 , а
, а 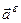 напрямлено перпендикулярно до площини, яка утворена векторами
напрямлено перпендикулярно до площини, яка утворена векторами 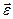 і
і 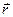 . Вектори
. Вектори  і
і 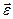 мають різні напрями, і загалом дані площини не співпадають.
мають різні напрями, і загалом дані площини не співпадають.
Векторний добуток 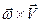 називається доосьовим пришвидшенням і позначається
називається доосьовим пришвидшенням і позначається 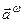 , тобто:
, тобто:
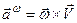 . (2.88)
. (2.88)
Його величина

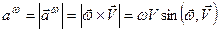 .
.
Оскільки вектори  і
і 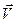 взаємно перпендикулярні (див. попередній параграф) і
взаємно перпендикулярні (див. попередній параграф) і 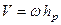 , отримаємо
, отримаємо
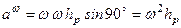 .
.
Отже,
доосьове пришвидшення точки тіла, яке здійснює сферичний рух, чисельно дорівнює добутку квадрата кутової швидкості тіла на відстань даної точки до миттєвої осі обертання
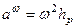 . (2.89)
. (2.89)
Щодо напряму цього пришвидшення, то воно перпендикулярне до площини побудованого на векторах  і
і 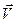 прямокутника (рис. 142), де для побудови цього прямокутника вектор
прямокутника (рис. 142), де для побудови цього прямокутника вектор  умовно зображено в точці
умовно зображено в точці  . Перпендикуляром до цієї площини є відрізок
. Перпендикуляром до цієї площини є відрізок 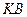 , тобто перпендикуляр, який опущений з точки
, тобто перпендикуляр, який опущений з точки  на миттєву вісь обертання. Отже, вектор доосьового пришвидшення напрямлений вздовж перпендикуляра, опущеного з точки, пришвидшення якої визначається, на миттєву вісь обертання. За визначенням векторного добутку легко переконатись, що цей вектор буде напрямлений до миттєвої осі обертання. Ось чому він називається доосьовим. Враховуючи введені позначення, формула (а) набуває вигляду
на миттєву вісь обертання. Отже, вектор доосьового пришвидшення напрямлений вздовж перпендикуляра, опущеного з точки, пришвидшення якої визначається, на миттєву вісь обертання. За визначенням векторного добутку легко переконатись, що цей вектор буде напрямлений до миттєвої осі обертання. Ось чому він називається доосьовим. Враховуючи введені позначення, формула (а) набуває вигляду

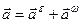 , (2.90)
, (2.90)
тобто,
пришвидшення точки твердого тіла, яке обертається навколо нерухомої точки, дорівнює геометри-чній сумі її обертального і доосьового пришвидшень.
Цю тезу часто називають теоремою Рівальса.
Загалом вектори обертального і доосьового пришвидшень не перпендикулярні один до одного, а тому величину пришвидшення 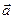 вираховують як діагональ паралелограма, який будується на векторах
вираховують як діагональ паралелограма, який будується на векторах 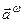 і
і 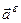 (рис. 143) за формулою
(рис. 143) за формулою

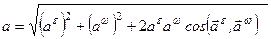 . (2.91)
. (2.91)
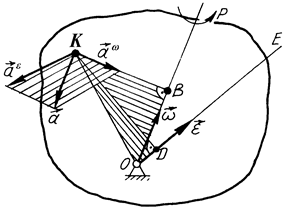
Рис. 143
Питання для самоконтролю
1. Скільки ступенів вільності має тверде тіло, що обертається навколо нерухомої точки?
2. Чому обертання твердого тіла навколо нерухомої точки називають сферичним рухом?
3. Запишіть рівняння обертання твердого тіла навколо нерухомої точки.
4. Що називається кутовою швидкістю твердого тіла, яке обертається навколо нерухомої точки?
5. Сформулюйте теорему Ейлера-Даламбера.
6. Як зображується вектор кутової швидкості твердого тіла, що обертається навколо нерухомої точки?
7. Запишіть формули, за допомогою яких можна визначити вектор кутового пришвидшення тіла, що обертається навколо нерухомої точки.
8. Чому в кожний момент часу вектор швидкості точки тіла, котре здійснює сферичний рух, можна визначити за формулою Ейлера?
9. Запишіть формулу Ейлера, яка визначає вектор швидкості точки тіла в обертальному русі.
10. За якою формулою визначається величина швидкості точки тіла, котре здійснює сферичний рух?
11. Запишіть формули, які визначають проекції на нерухомі осі координат вектора швидкості точки тіла, яке здійснює сферичний рух.
12. Сформулюйте теорему Рівальса.
13. За якою формулою визначається величина доосьового пришвидшення?
14. За якою формулою визначається величина обертального пришвидшення точки тіла в сферичному русі?
15. Тіло обертається навколо нерухомої точки. В даний момент часу проекції вектора кутової швидкості на нерухомі осі координат мають значення: 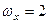 с–1,
с–1, 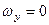 ,
, 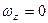 . Що в даний момент часу є миттєвою віссю обертання тіла?
. Що в даний момент часу є миттєвою віссю обертання тіла?
16. В деякий момент часу тіло, яке обертається навколо нерухомої точки, має кутову швидкість 2 с–1, кутове пришвид-шення 3 с–2. Вектор кутової швидкості в даний момент часу напрямлений вздовж осі абсцис, а вектор кутового пришвидшення – вздовж осі ординат. Знайти величину швидкості точки М (0,4; 0,3; 0). Координати точок задані в метрах. Початок системи координат знаходиться в нерухомій точці тіла.
17. За умовою питання №16 визначити доосьове пришвидшення точки М.
18. За умовою питання №16 знайти величину обертального пришвидшення точки М.
19. За умовою питання №16 вказати напрям вектора швидкості точки М.
20. За умовою питання №16 вказати напрям вектора доосьового пришвидшення точки М.
21. За умовою питання №16 вказати напрям вектора обертального пришвидшення точки М.
§ 48 Рух вільного твердого тіла
Розглянемо рух вільного твердого тіла, тобто тіла, рух якого не обмежений в’язями. Для визначення його положення в просторі введемо такі системи координат (рис. 144): 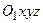 – нерухому систему координат;
– нерухому систему координат; 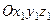 – рухому систему координат, яка рухається поступально відносно осей
– рухому систему координат, яка рухається поступально відносно осей 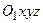 і з’єд-нана з тілом тільки однією точкою – точкою
і з’єд-нана з тілом тільки однією точкою – точкою  ;
; 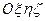 – рухому систему координат, яка жорстко з’єднана з твердим тілом. В рухомій системі координат
– рухому систему координат, яка жорстко з’єднана з твердим тілом. В рухомій системі координат 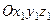 тіло має одну закріплену (нерухому) точку – точку
тіло має одну закріплену (нерухому) точку – точку  , отже, тіло в даній системі координат здійснює рух, розглянутий в попередньому параграфі, згідно з яким положення тіла в даній системі координат можна визначити кутами Ейлера
, отже, тіло в даній системі координат здійснює рух, розглянутий в попередньому параграфі, згідно з яким положення тіла в даній системі координат можна визначити кутами Ейлера 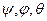 . Для визначення положення тіла відносно нерухомої системи координат
. Для визначення положення тіла відносно нерухомої системи координат 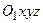 треба, крім цього, задати положення точки
треба, крім цього, задати положення точки  , а для цього потрібні ще три величини:
, а для цього потрібні ще три величини: 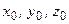 – координати точки
– координати точки  в нерухомій системі координат. Таким чином, положення вільного твердого тіла визначається шістьма параметрами:
в нерухомій системі координат. Таким чином, положення вільного твердого тіла визначається шістьма параметрами: 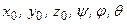 . Функціональна залежність даних параметрів від часу
. Функціональна залежність даних параметрів від часу
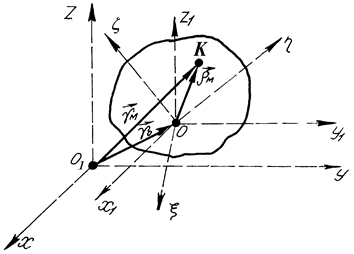
Рис. 144
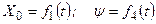 ;
;
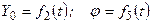 ; (2.92)
; (2.92)
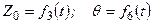
визначатиме рівняння руху вільного твердого тіла, бо за допомогою цих рівнянь можна визначити положення тіла в будь-який момент часу.
Звернемо увагу на те, що рух вільного твердого тіла є складним. Він складається з поступального руху разом з деякою точкою, яка називається, як і в плоскопаралельному русі полюсом, і обертання навколо даної точки. І дійсно, в частковому випадку, коли
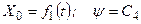 ;
;
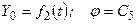 ; (2.92)
; (2.92)
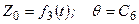 ,
,
де 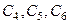 – деякі константи, отримаємо поступальний рух твердого тіла. А у випадку, коли
– деякі константи, отримаємо поступальний рух твердого тіла. А у випадку, коли
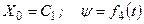 ;
;
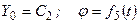 ;
;
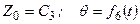 ,
,
тіло буде обертатись навколо нерухомої точки.
Оскільки за полюс можна взяти будь-яку точку твердого тіла, то, вибираючи різні точки тіла за полюс, отримаємо безліч розкладень руху вільного тіла на поступальну і обертальну частини. Легко довести, що поступальна частина руху залежить від вибору полюса, а обертальна – не залежить. Це саме було отримано для плоскопаралельного руху (див. § 46.2).
Для обертального руху твердого тіла навколо точки  згідно з попереднім параграфом в кожний момент часу існує миттєва вісь обертання, яка проходить через точку
згідно з попереднім параграфом в кожний момент часу існує миттєва вісь обертання, яка проходить через точку  . Отже, в кожний момент часу рух вільного тіла можна розглядати, як сукупність двох рухів: поступального разом з деякою точкою і обертального навколо деякої миттєвої осі, яка проходить через дану точку.
. Отже, в кожний момент часу рух вільного тіла можна розглядати, як сукупність двох рухів: поступального разом з деякою точкою і обертального навколо деякої миттєвої осі, яка проходить через дану точку.
Перейдемо до визначення швидкостей точок вільного тіла. Швидкість довільної точки  дорівнює похідній за часом від радіуса-вектора
дорівнює похідній за часом від радіуса-вектора 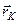 , який визначає її положення в нерухомій системі відліку. На підставі рис. 144 маємо
, який визначає її положення в нерухомій системі відліку. На підставі рис. 144 маємо
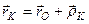 .
.
Отже,
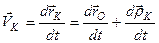 .
.
Оскільки 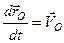 – швидкість точки
– швидкість точки  , а похідна
, а похідна 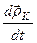 є швидкість точки
є швидкість точки  відносно точки
відносно точки  –
– 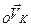 , то отримуємо
, то отримуємо
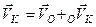 . (2.93)
. (2.93)
Отриману формулу можна прочитати так:
швидкість будь-якої точки вільного тіла дорівнює геометричній сумі швидкості довільно вибраного полюса і швидкості даної точки в обертальному русі тіла навколо полюса.
Продиференціювавши векторну рівність (2.93) за часом
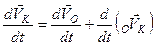
і знаючи, що перша похідна за часом від вектора лінійної швидкості визначає вектор відповідного лінійного пришвидшення, отримаємо
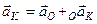 , (2.94)
, (2.94)
тобто:
пришвидшення будь-якої точки вільного тіла дорів-нює геометричній сумі пришвидшення полюса і при-швидшення даної точки в обертальному русі тіла навколо полюса.
Таким чином, отримано формули, які дають змогу обчислювати швидкість (формула 2.93) і пришвидшення (формула 2.94) будь-якої точки вільного тіла. В даних формулах вектори 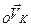 і
і 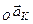 визначається так, як було вказано в попередньому параграфі.
визначається так, як було вказано в попередньому параграфі.
Питання для самоконтролю
1. Яке тверде тіло називається вільним?
2. Скільки ступенів вільності має вільне тверде тіло?
3. Скільки незалежних параметрів необхідно для однозначного визначення положення вільного тіла в просторі?
4. Запишіть рівняння руху вільного твердого тіла.
5. Що називається полюсом вільного твердого тіла?
6. З яких рухів складається рух вільного твердого тіла?
7. Як залежать складові рухи вільного твердого тіла від вибору полюса?
8. Запишіть і прочитайте формулу, за допомогою якої визначається швидкість точки вільного тіла.
9. Запишіть і прочитайте формулу, за допомогою якої визначається пришвидшення точки вільного тіла.
10. В деякий момент часу пришвидшення точки  вільного тіла визначається виразом
вільного тіла визначається виразом 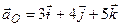 . В цей момент часу кутова швидкість тіла
. В цей момент часу кутова швидкість тіла 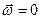 , кутове пришвидшення
, кутове пришвидшення 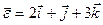 . Знайти пришвидшення точки
. Знайти пришвидшення точки  тіла, якщо
тіла, якщо 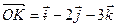 .
.
11. Рух вільного тіла описується рівняннями 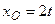 ,
, 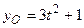 ,
, 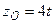 ,
, 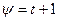 ,
, 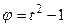 ,
, 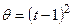 . Знайти в момент часу
. Знайти в момент часу 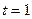 с швидкість полюса, якщо
с швидкість полюса, якщо 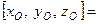 м,
м, 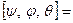 рад.
рад.
12. Тіло вільно рухається в просторі згідно з рівняннями 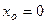 ,
, 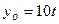 м,
м, 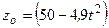 м,
м, 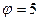 рад,
рад, 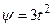 рад,
рад, 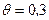 рад. Визначить модуль кутової швидкості тіла в момент часу
рад. Визначить модуль кутової швидкості тіла в момент часу 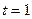 с.
с.
13. Знайти проекцію на нерухому вісь абсцис швидкості точки  вільного тіла, якщо її радіус-вектор відносно полюса
вільного тіла, якщо її радіус-вектор відносно полюса 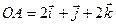 , миттєва кутова швидкість
, миттєва кутова швидкість 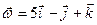 , а рівняння руху полюса
, а рівняння руху полюса 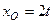 ,
, 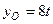 ,
, 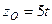 . Всі величини в системі СІ.
. Всі величини в системі СІ.
§ 49 Синтез рухів
Тут для розгляду складного руху твердого тіла застосовуємо метод синтезу, тобто складний рух твердого тіла отримаємо способом складання його найпростіших рухів. Основною метою даного параграфа є визначення результуючого руху твердого тіла, яке здійснює одночасно два або декілька простих рухів і отримання залежностей між кінематичними характеристиками результуючого і складових рухів.
§ 49.1 Складання поступальних рухів твердого тіла
Нехай тверде тіло одночасно здійснює два поступальні рухи. Прикладом такого руху є рух поршня автомобільного двигуна. І дійсно, поршень автомобільного двигуна рухається поступально відносно циліндра двигуна і одночасно рухається з автомобілем, який також здійснює поступальний рух.
 Для визначення результуючого руху розглянемо тверде тіло, яке рухається поступально з швидкістю
Для визначення результуючого руху розглянемо тверде тіло, яке рухається поступально з швидкістю 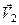 відносно рухомої системи координат
відносно рухомої системи координат 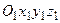 , яка в свою чергу рухається також поступально зі шви-дкістю
, яка в свою чергу рухається також поступально зі шви-дкістю 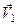 відносно нерухомої системи координат
відносно нерухомої системи координат 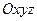 (рис. 145). Визначимо швидкості двох довільних точок тіла, наприклад, точок
(рис. 145). Визначимо швидкості двох довільних точок тіла, наприклад, точок  і
і  . Оскільки тіло здійснює складний рух, то його точки також здійснюють складний рух. За теоремою про складання швидкостей (див. формулу 2.58) маємо
. Оскільки тіло здійснює складний рух, то його точки також здійснюють складний рух. За теоремою про складання швидкостей (див. формулу 2.58) маємо
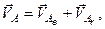
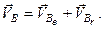 (а)
(а)
За переносний рух тіла приймаємо його рух разом з рухомою системою координат 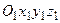 . Оскільки рухома система координат рухається поступально зі швидкістю
. Оскільки рухома система координат рухається поступально зі швидкістю 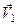 , то переносний рух тіла є поступальним, а це означає, що переносні швидкості всіх точок є однаковими і рівними
, то переносний рух тіла є поступальним, а це означає, що переносні швидкості всіх точок є однаковими і рівними 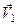 , тобто
, тобто
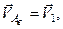
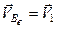 . (б)
. (б)
Відносним рухом тіла є його рух відносно рухомої системи координат зі швидкістю 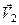 . Цей рух є також поступальним, отже і відносні швидкості всіх точок тіла будуть однаковими і рівними, тобто:
. Цей рух є також поступальним, отже і відносні швидкості всіх точок тіла будуть однаковими і рівними, тобто:
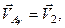
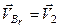 . (в)
. (в)
Підставляючи (б) і (в) в рівності (а), отримуємо
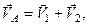
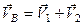 ,
,
тобто:
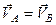 .
.
Оскільки точки  і
і  в твердому тілі вибрані довільно, то можна зробити висновок, що абсолютні швидкості всіх точок тіла геометрично рівні, а це означає, що абсолютний (результуючий) рух твердого тіла є поступальним.
в твердому тілі вибрані довільно, то можна зробити висновок, що абсолютні швидкості всіх точок тіла геометрично рівні, а це означає, що абсолютний (результуючий) рух твердого тіла є поступальним.
Отже,
при складанні двох поступальних рухів твердого тіла результуючий рух тіла є поступальним зі швидкістю, яка дорівнює геометричній сумі швидкостей складових рухів
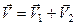 , (2.95)
, (2.95)
У випадку 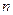 поступальних рухів, користуючись принципом незалежності рухів (див. курс фізики) і застосовуючи послідовно попередні міркування, отримаємо, що результуючий рух також буде поступальним, а його швидкість буде дорівнювати геометричній сумі швидкостей складових рухів, тобто
поступальних рухів, користуючись принципом незалежності рухів (див. курс фізики) і застосовуючи послідовно попередні міркування, отримаємо, що результуючий рух також буде поступальним, а його швидкість буде дорівнювати геометричній сумі швидкостей складових рухів, тобто
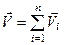 . (2.96)
. (2.96)
Якщо швидкості всіх точок тіла геометрично рівні тільки в деякий момент часу, то рух в такому випадку називається миттєво-поступальним. Миттєво-поступальний рух твердого тіла відрізняється тим, що в даному русі геометрично рівні тільки швидкості всіх точок тіла, а пришвидшення різні, тобто
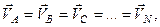
але
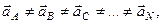
тоді як при поступальному русі тіла швидкості і пришвидшення всіх його точок геометрично рівні.
§ 49.2 Складання поступального і обертального рухів
твердого тіла
Розглянемо складний рух твердого тіла, який складається з поступального і обертального навколо деякої осі. Тут можуть зустрітись такі випадки: вектор швидкості поступального руху є: а) перпендикулярним до осі обертання; б) паралельним до осі обертання; в) утворює з віссю обертання довільний кут. Розглянемо окремо кожний з цих випадків.
а) Швидкість поступального руху перпендикулярна до осі обертання
Прикладом такого руху є рух автомобільних коліс, які рухаються поступально разом з автомобілем і одночасно обертаються навколо відповідних осей, до того ж в кожний момент часу швидкість поступального руху перпендикулярна до осі обертання колеса.
Припустимо, що тіло 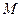 обертається з кутовою швидкістю
обертається з кутовою швидкістю  навколо осі
навколо осі 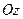 , яка жорстко скріплена з іншим тілом (наприклад, з площиною
, яка жорстко скріплена з іншим тілом (наприклад, з площиною 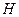 ), яке рухається поступально зі швидкістю
), яке рухається поступально зі швидкістю 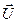 , перпендикулярною до осі
, перпендикулярною до осі 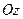 (рис. 146). Для визначення результуючого руху на осі
(рис. 146). Для визначення результуючого руху на осі 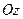 візьмемо довільну точку
візьмемо довільну точку 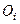 , через яку проведемо осі
, через яку проведемо осі 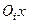 і
і 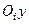 , причому вісь
, причому вісь 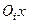 проведемо паралельно до вектора
проведемо паралельно до вектора 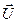 . На осі
. На осі 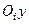 візьмемо точку
візьмемо точку 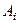 на відстані
на відстані
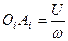 (а)
(а)
і визначимо її швидкість. Тіло 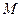 здійснює складний рух, отже кожна його точка здійснює складний рух, а це означає, що швидкість точки
здійснює складний рух, отже кожна його точка здійснює складний рух, а це означає, що швидкість точки 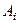 можна обчислити за формулою
можна обчислити за формулою
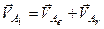 . (б)
. (б)
За переносний рух приймемо поступальний рух твердого тіла, тоді переносна швидкість кожної точки тіла буде дорівнювати 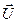 , тобто:
, тобто:
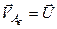 . (в)
. (в)
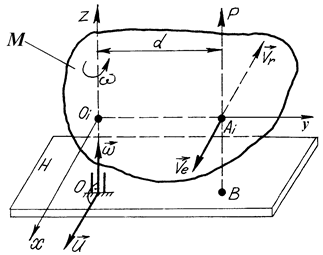
Рис. 146
За відносний рух приймемо обертання твердого тіла навколо осі 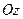 , тоді величина відносної швидкості кожної точки тіла буде дорівнювати добутку кутової швидкості на відстань даної точки до осі обертання. Для точки
, тоді величина відносної швидкості кожної точки тіла буде дорівнювати добутку кутової швидкості на відстань даної точки до осі обертання. Для точки 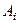 , враховуючи співвідношення (а), отримаємо
, враховуючи співвідношення (а), отримаємо
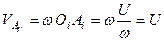 . (г)
. (г)
Вектор відносної швидкості як вектор обертальної швидкості буде перпендикулярним до відповідного радіуса. Для точки 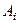
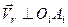 і напрямлений в бік обертання, як вказано на рис. 146.
і напрямлений в бік обертання, як вказано на рис. 146.
Підставляючи (в) і (г) у формулу (б) і враховуючи, що вектори  і
і 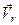 напрямлені по одній прямій в протилежні боки, отримаємо
напрямлені по одній прямій в протилежні боки, отримаємо
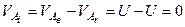 ,
,
тобто абсолютна швидкість точки 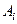 в даний момент часу дорівнює нулеві.
в даний момент часу дорівнює нулеві.
Якщо через точку 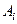 паралельно до осі
паралельно до осі 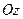 провести вісь
провести вісь 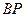 і врахувати, що на осі
і врахувати, що на осі 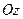 точку
точку 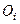 вибрано довільно (отже, і точка
вибрано довільно (отже, і точка 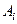 є довільною точкою осі
є довільною точкою осі 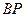 ), то можна зробити такий висновок: вісь
), то можна зробити такий висновок: вісь 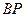 є геометричне місце точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла в даний момент часу є обертальним.
є геометричне місце точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла в даний момент часу є обертальним.
Таким чином,
при складанні поступального і обертального рухів твердого тіла у випадку, коли швидкість поступального руху перпендикулярна до осі обертання, результуючий рух тіла в кожний момент часу є обертальним навколо миттєвої осі обертання, паралельної до осі обертання складового руху, і знаходиться від неї на відстані d, яка визначається за формулою
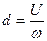 . (2.97)
. (2.97)
Відрізок 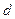 відкладається вздовж перпендикуляра до площини, яка проходить через вектори
відкладається вздовж перпендикуляра до площини, яка проходить через вектори  і
і 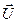 в бік, звідки поворот вектора
в бік, звідки поворот вектора  до
до 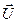 на кут
на кут 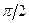 видно проти руху годинникової стрілки.
видно проти руху годинникової стрілки.
Позначимо кутову швидкість результуючого (абсолютною) руху 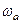 і визначимо її. Для цього за формулою
і визначимо її. Для цього за формулою
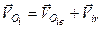 (д)
(д)
визначимо абсолютну швидкість точки 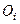 . Кожний з векторів які входять в рівність (д), легко обчислити:
. Кожний з векторів які входять в рівність (д), легко обчислити:
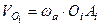 , адже абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі
, адже абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі 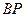 ;
;
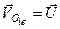 , бо переносний рух, як було прийнято, є поступальним зі швидкістю
, бо переносний рух, як було прийнято, є поступальним зі швидкістю 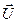 ;
;
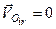 , точка
, точка 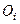 знаходиться на осі відносного обертання.
знаходиться на осі відносного обертання.
Враховуючи все це, з рівності (д) отримаємо
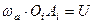 .
.
Звідки, враховуючи формулу (а), матимемо
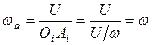 ,
,
кутова швидкість результуючого (абсолютного) руху дорівнює кутовій швидкості складового обертання.
На закінчення звернемо увагу на те, що цей вид руху тіла є не що інше як плоскопаралельний рух, який, як відомо, визначається рухом плоскої фігури в її площині. Саму плоску фігуру отримаємо шляхом перетину тіла площиною, перпендикулярною до осі 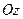 . Миттєвий центр швидкостей, навколо якого плоска фігура в даний момент часу здійснює обертальний рух, буде знаходитися в точці її перетину з миттєвою віссю (
. Миттєвий центр швидкостей, навколо якого плоска фігура в даний момент часу здійснює обертальний рух, буде знаходитися в точці її перетину з миттєвою віссю ( 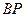 ) обертання тіла.
) обертання тіла.
б) Швидкість поступального руху паралельна
осі обертання
 Прикладом такого руху є рух свердла свердлильного верстата, рух гайки при закручуванні її на болт, рух гвинта при польоті літака і т.п.
Прикладом такого руху є рух свердла свердлильного верстата, рух гайки при закручуванні її на болт, рух гвинта при польоті літака і т.п.
На рис. 147 зображено тіло
