Складання обертань навколо паралельних осей

Прикладом одночасного обертання тіла навколо двох паралельних осей є рух зубчастого колеса 2, котре перебуває у зчепленні з нерухомим колесом 1 і приводиться в рух кривошипом 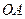(рис. 151). Аналіз руху колеса 2 показує, що воно одночасно здійснює два обертання: обертається разом з кривошипом 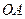навколо осі 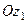з кутовою швидкістю 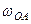, а щоб здійснювати цей рух, то воно ще обертається навколо осі 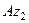з деякою кутовою швидкістю 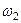. 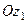Осі і 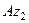перпендикулярні до площин коліс, тобто вони є паралельними.

При складанні обертань навколо паралельних осей можуть бути такі випадки: а) обертання напрямлені в один бік; б) обертання напрямлені в протилежні боки і здійснюються з різними за величиною кутовими швидкостями; в) обертання напрямлені в протилежні боки і здійснюється з однаковими за величиною кутовими швидкостями.

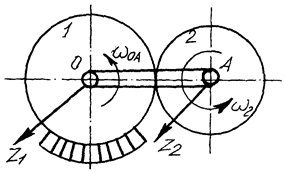
Рис. 151

Розглянемо окремо кожний з цих випадків.

а) Обертання напрямлені в один бік

Нехай тверде тіло обертається навколо осі з кутовою швидкістю , а сама вісь 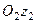обертається навколо паралельної їй осі 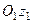з кутовою швидкістю 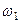(рис. 152). Обертання навколо осей 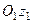і 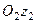, як видно з цього рисунка, напрямлені в один бік. Для визначення результуючого руху твердого тіла 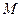, яке при заданій постановці задачі одночасно обертається навколо двох паралельних осей (ос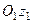і і 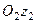), з довільної точки 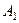осі 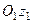перпендикулярно до осей обертання проведемо відрізок прямої 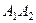. На цьому відрізку беремо точку , яка ділить даний відрізок у співвідношенні

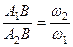(а)

і визначимо її швидкість. Точка здійснює складний рух, бо належить тілу 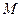, яке здійснює складний рух, отже її швидкість можна визначити за теоремою про складання швидкостей

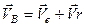. (б)

Якщо обертання тіла навколо осі 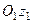прийняти за переносний рух, а навколо осі 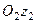– за відносний, то матимемо:

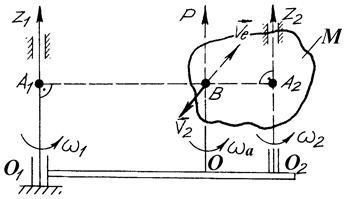
Рис. 152

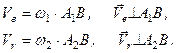(в)

Вектори даних швидкостей напрямлені в боки відповідних обертань і, як видно з рис. 152, вони є протилежними, а це означає, що векторна сума (б) перетворюється в алгебраїчну різницю

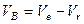
і, враховуючи (в) і (а), отримаємо

.

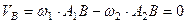Абсолютна швидкість точки в даний момент часу дорівнює нулеві.

Якщо через точку паралельно заданим осям 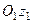і 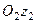провести вісь 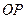і врахувати, що на осі 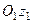точку 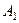вибрано довільно (отже, і точка є довільною точкою осі 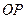), то можна зробити такий висновок: вісь 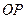є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання тіла, а це означає, що результуючий рух твердого тіла є обертальним.

Таким чином,

при складанні обертальних рухів твердого тіла на-вколо двох паралельних осей у випадку, коли обертання напрямлені в один бік, результуючий (абсолютний) рух є обертальним в той самий бік навколо миттєвої осі обертання, яка розміщена в площині, що проходить через осі обертань складових рухів, паралельно до них, і ділить відстань між ними внутрішнім чином на відрізки, котрі обернено пропорційні кутовим швидкостям складових рухів

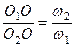. (2.104)

Позначимо кутову швидкість результуючого (абсолютного) обертання 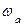і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки 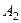тіла 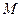(рис. 152)

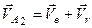. (г)

В записаній рівності:

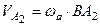, бо абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі обертання ;

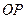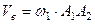, бо переносний рух, як було прийнято вище, є обертальним навколо осі 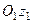(рис. 152);

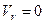, точка 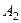знаходиться на осі відносного обертання .

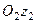Враховуючи це, рівність (г) набуває вигляду

.

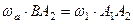Звідси матимемо

.

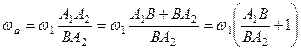Якщо замість відношення 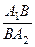підставити його значення з (а), то остаточно отримуємо

,

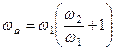тобто:

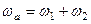. (2.105)

Кутова швидкість абсолютного обертання дорівнює сумі кутових швидкостей складових рухів.

б) Обертання напрямлені в протилежні боки і здійсню-ються з різними за величиною кутовими швидкостями

Нехай тверде тіло 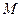обертається навколо осі 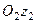з кутовою швидкістю 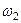, а сама вісь 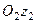обертається навколо паралельної до неї осі 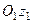з кутовою швидкістю 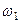(рис. 153). Обертання навколо осей 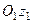і 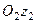, як видно з цього рисунка, напрямлені в протилежні боки. Припустимо, що 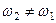, і нехай .

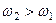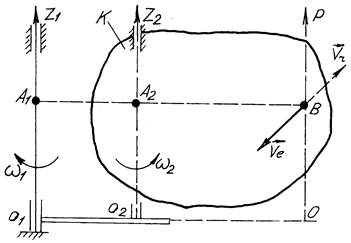
Рис. 153

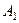Для визначення результуючого руху твердого тіла , яке при заданій постановці задачі одночасно обертається нав-коло двох паралельних осей в протилежні боки, як і в попередньому випадку, з довільної точки осі 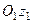перпендикулярно до осей обертання проведемо відрізок 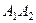. На продовженні цього відрізка (продовження проводимо за вісь, навколо якої тіло обертається з більшою кутовою швидкістю; в даному випадку це вісь 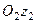) беремо точку , положення якої визначається співвідношенням

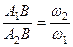, (а)

і за теоремою про складання швидкостей визначимо її швидкість

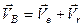. (б)

Якщо обертання тіла навколо осі 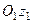прийняти за переносний рух, а навколо осі 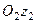– за відносний, то матимемо

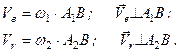(в)

Вектори і 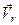напрямлені в боки відповідних обертань, як видно з рис. 153, вони є протилежними, а це означає, що векторна сума (б) перетворюється в алгебраїчну різницю

,

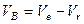і, враховуючи (в) і (а), отримаємо

,

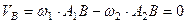абсолютна швидкість точки в даний момент часу дорівнює нулеві.

Якщо через точку паралельно заданим осям 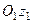і 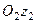провести вісь 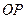і врахувати, що на осі 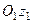точку 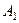вибрано довільно (отже, і точка є довільною точкою осі 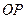), то можна зробити такий висновок: вісь 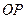є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла є обертальним.

Таким чином,

при складанні обертальних рухів твердого тіла на-вколо двох паралельних осей у випадку, коли обертання напрямлені в протилежні боки і здійснюються з різними за величиною кутовими швидкостями, результуючий (абсолютний) рух є обертальним в бік більшої кутової швидкості навколо осі обертання, яка розміщена в площині, що проходить через осі обертань складових рухів, паралельна до них і ділить відстань 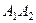між ними зовнішнім чином на відрізки, котрі обернено пропорційні кутовим швидкостям складових рухів

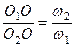. (2.106)

Позначимо кутову швидкість результуючого обертання 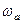і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки 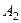тіла 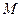(рис. 153)

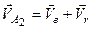. (г)

Оскільки переносний, відносний і абсолютний рухи твердого тіла є обертальними, то:

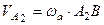, адже в абсолютному русі тіло в даний момент часу обертається навколо осі ;

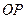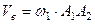– за переносний рух прийнято обертання навколо осі ;

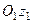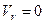, точка 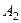знаходиться на відносній осі обертання.

Враховуючи це, рівняння (г) набуває вигляду

.

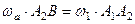Звідси матимемо

.

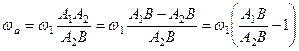Якщо замість відношення 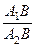підставити його значення з (а), то отримаємо

,

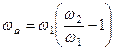тобто:

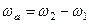. (2.107)

Кутова швидкість абсолютного обертання дорівнює різниці кутових швидкостей складових рухів.

Зауважимо, що при визначенні кутової швидкості абсолютного обертання за формулою (2.107) від більшої кутової швидкості віднімається менша, а це означає, що результуюча кутова швидкість як вектор буде напрямлена в бік більшої кутової швидкості.

в) Обертання напрямлені в протилежні боки і здій-снюються з однаковими за величиною кутовими швидкостями (пара обертань)

Розглянемо тепер складний рух твердого тіла, який складається з двох обертань навколо паралельних осей 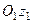і 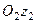(рис. 154). Нехай обертання, як і в попередньому випадку, напрямлені в протилежні боки, але здійснюються з однаковими за величиною кутовими швидкостями, а це означає, що вектори кутових швидкостей задовольняють умову 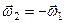. Така сукупність рухів часто називається парою обертання (кінематичною парою).

Отже,

пара обертань – це сукупність двох обертань твердого тіла навколо паралельних осей з рівними за величиною, але протилежними за напрямом кутовими швидкостями.

Для визначення результуючого руху за теоремою про складання швидкостей обчислимо швидкість довільної точки тіла, положення якої відносно точок 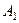і 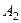осей обертання визначається радіусами-векторами 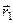і 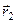(рис. 154).

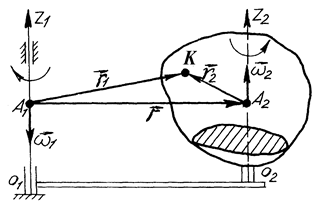
Рис. 154

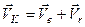, (а)

Оскільки переносний і відносний рухи є обертальними відповідно з кутовими швидкостями 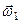і 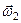, то вектори переносної і відносної 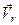швидкостей можна обчислювати за формулою Ейлера

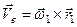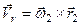, . (б)

Підставивши (б) і рівність (а), отримаємо

.

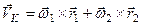Якщо врахувати, що 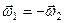, то матимемо

.

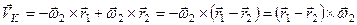Оскільки 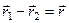(див. рис. 154), то

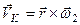. (2.108)

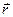Оскільки швидкість точки не залежить від її положення (вектори і 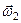не з’єднані з точкою ), то швидкості всіх точок тіла в даний момент часу геометрично рівні між собою, а це означає, що тіло здійснює поступальний рух.

Таким чином,

при складанні двох обертань твердого тіла навколо паралельних осей з рівними за величиною, але протилежними за напрямом кутовими швидкостями результуючий рух є поступальним,

тобто пара обертань 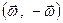еквівалентна миттєвому поступальному руху з швидкістю, що дорівнює моменту пари обертань. І дійсно, за аналогією зі статикою (див. теорію пари сил §16), векторний добуток 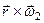можна назвати моментом пари обертань, тобто:

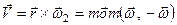. (2.109)

З рівності (2.109) випливає:

1) швидкість поступального руху 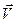перпендикулярна до площини пари і напрямлена так, що спостерігач з кінця 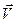бачить вектори пари 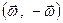, що намагаються повернути площину проти руху годинникової стрілки (рис. 155);

Рис. 155

2) величина цієї швидкості визначається формулою

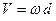, (2.110)

в якій – плече пари обертання.

Прикладом пари обертань є рух педалі велосипеда (рис. 156). Педаль велосипеда бере участь у двох обертаннях протилежного напряму: разом з кривошипом обертається навколо осі обертання великої зубчастої зірочки і одночасно обертається навколо власної осі (пальця кривошипа). Ці обертання здійснюються з однаковими за модулем кутовими швидкостями ( ), адже за час одного оберту кривошипа педаль відносно кривошипа зробить також один оберт, тільки в протилежному напрямі. В результаті складання цих обертань отримується поступальний рух, підтвердженням цього є те, що педаль за час руху велосипеда нахилена під певним, до того ж сталим, кутом до полотна дороги, а це означає, що всяка пряма, проведена в педалі, залишається собі паралельною, що є характерним для поступального руху твердого тіла.

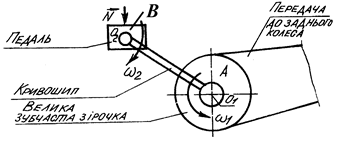
Рис. 156

Резюме. При складанні обертальних рухів як навколо осей, що перетинаються, так і навколо паралельних осей результуючий рух в кожний момент часу переважно є обертальним; тільки для пари обертань результуючий рух є поступальним.

На підставі доведеного можна розв’язувати такі задачі:

1. Складний рух твердого тіла, який складається з 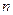обертальних рухів навколо осей, що перетинаються в одній точці, або навколо паралельних осей, в кожний момент часу звести до одного (обертального або поступального) руху, тобто звести до канонічного вигляду.

2. Кожний обертальний рух твердого тіла розкласти на 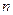обертань навколо осей, що перетинаються в одній точці, або навколо паралельних осей.

3. Кожний поступальний рух твердого тіла замінити парою миттєвих обертань. До того ж існує нескінченна кількість таких перетворень, але кожне з них повинно задовольняти рівність (2.109).

Питання для самоконтролю

1. Який рух твердого тіла називається складним?

2. Чи можна складанням поступальних рухів твердого тіла отримати обертальний рух тіла?

3. Тіло одночасно приймає участь у двох поступальних рухах, швидкості яких 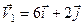, 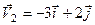. Знайти модуль абсолютної швидкості тіла.

4. Тіла 1, 2, 3 здійснюють поступальні рухи, як вказано на рисунку. Знайти в момент часу 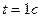абсолютну швидкість тіла 3, якщо , , .

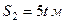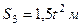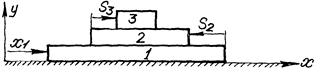
5. В прикладі 4 визначити відносну швидкість тіла 3 відносно тіла 1.

6. Який результуючий рух тіла отримується при складанні поступального і обертального рухів у випадку, коли вектор швидкості поступального руху перпендикулярний до осі обертання?

7. Квадрат зі стороною
60 см рухається поступально з швидкістю 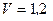м/с і одночасно обертається навколо осі 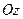з кутовою швидкістю 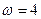с^–1. Знайдіть положення миттєвої осі абсолютного обертання квадрата, якщо 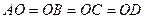, 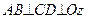. Яка кутова швидкість абсолютного обертання?

8. В якому випадку при складанні простих рухів отримується гвинтовий рух?

9. Що називається кроком кінематичного гвинта? Запишіть формулу, за допомогою якої визначається крок кінематичного гвинта.

10. Чи можна складанням обертальних рухів тіла отримати його поступальний рух? Якщо так, то в якому випадку?

11. Тіло одночасно обертається навколо двох паралельних осей з кутовими швидкостями 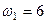с^–1, с^–1. Обер-тання напрямлені в один бік. Який результуючий рух тіла? Яка швидкість результуючого руху?

12. Тіло одночасно обертається навколо двох паралельних осей з кутовими швидкостями 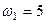с^–1, 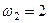с^–1. Обер-тання напрямлені в різні боки. Який результуючий рух тіла? Яка швидкість результуючого тіла?

13. Що називається парою обертання? Який результуючий рух дає пара обертань? Яка швидкість результуючого руху?

14. Яким буде абсолютний рух тіла, котре одночасно обертається навколо двох осей, що перетинаються, з кутовою швидкостями 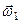і 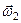? Яка швидкість результуючого руху?

15. Тіло одночасно обертається навколо чотирьох осей, які напрямлені вздовж сторін прямокутника 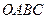, як вказано на рис. А. Яким буде результуючий рух тіла і яка швидкість результуючого руху, якщо с^–1, с^–1?

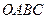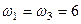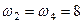16. Тіло одночасно обертається навколо чотирьох осей, які напрямлені вздовж сторін прямокутника , як вказано на рис. Б. Яким буде результуючий рух, якщо с^–1, с^–1?

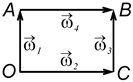Рис. А

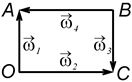Рис. Б

17. Тіло обертається навколо осі 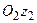з кутовою швидкістю 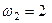с^–1 і одночасно навколо осі 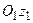з кутовою швидкістю 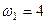с^–1, як вказано на рисунку. Ос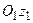і і 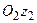паралельні. Вказати положення миттєвої осі обертання тіла, якщо 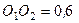м.

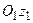18. Тіло одночасно обертається навколо двох паралельних осей і 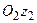, як вказано на рисунку. Який буде резу-льтуючий рух тіла, якщо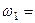 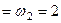с^–1, 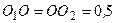? Визначити величину і вказати на рисунку вектор швидкості результуючого руху.

19. Диск обертається навколо вертикальної осі з кутовою швидкістю 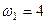с^–1 і навколо горизонтальної осі з кутовою швидкістю с^–1, як вказано на рисунку. Яким є результуючий рух диска і яка швидкість результуючого руху?

20. Тіло одночасно бере участь у двох обертаннях з кутовими швидкостями 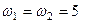с^–1, вектори яких напрямлені вздовж ребер куба з стороною 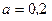м, як вказано на рисунку. Яким буде абсолютний рух тіла? Знайти кінематичні характеристики цього
руху.

§ 50 Аналогії між кінематикою і статикою

Одним з основних понять статики є поняття сили. Сила в статиці твердого тіла (див. § 6) є ковзним вектором. Іншим важливим поняттям статики є поняття про момент пари сил. Момент пари сил (див. § 17) є вільним вектором. Аналогічні вектори є і в кінематиці. Вектор кутової швидкості (див.
§ 43.4) є ковзним вектором. Вектор моменту пари обертань (див. § 49.4) є вільним вектором.

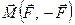Отже, між векторами і , і 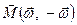є аналогія. Треба зауважити, що ця аналогія є зовнішньою (формальною), а не фізичною. Проте знання її необхідне для більш глибокого розуміння законів механічного руху і є ще одним підтвердженням взаємозв’язку цих законів. Оскільки дані вектори лежать в основі побудови теоретичного курсу статики твердого тіла і кінематики, то природно чекати, що і між теоремами цих розділів є також відповідна аналогія. Очевидно, аналогії треба шукати між теоремами, які мають голов-ним чином геометричний зміст і доведення яких базується на загальних властивостях ковзних і вільних векторів. Систематизація теорем дає таку картину аналогії.

№	Статика	Кінематика
	Аксіома про паралело- грам сил (§ 6)	Складання обертань твердого тіла навколо двох осей, що перетинаються (§ 49.3)
	Зведення збіжної системи сил до канонічного вигляду (§ 7)	Складання обертань твердого тіла навколо 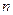осей, що перетинаються в одній точці (§ 49.3)
	Пара сил і її властивості (§ 16)	Пара обертань і її властивості (§ 49.4)
	Лема про паралельний перенос сили (§ 19)	Теорема про паралельний перенос вектора кутової швидкості
	Зведення довільної системи сил до канонічного вигляду (§ 20)	Теорема про складання поступальних і обертальних рухів
	Складання паралельних сил (курс фізики середньої школи, додаток 4)	Складання обертань тіла навколо паралельних осей (§ 49.4)

Як видно з таблиці, більшість з наведених теорем доведена вище. Під номерами 4 і 5 вказані нові, ще не доведені, теореми кінематики твердого тіла. Доведемо ці теореми в даному параграфі.

Теорему про паралельний перенос вектора кутової швидкості сформулюємо за аналогією леми про паралельний перенос сили:

не змінюючи миттєвого розподілу швидкостей в тілі, вектор кутової швидкості можна паралельно перенести в будь-яку точку, якщо при цьому приєднати пару обертань, момент якої геометрично дорівнює моменту заданої кутової швидкості відносно точки переносу.

Доведення даної теореми є по суті повторенням доведення аналогічної теореми статики. Нехай деяке тверде тіло (рис. 157, а) обертається навколо осі 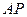з кутовою швидкістю . В точці до тіла вздовж осі 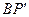, яка паралельна осі 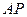, приєднаємо еквівалентну нулеві сукупність обертань 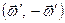так, що 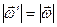(рис. 157, б). Вектори і 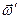утворюють пару обертань, яку за формулою (2.109) замінено вільним вектором-моментом пари обертань

.

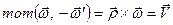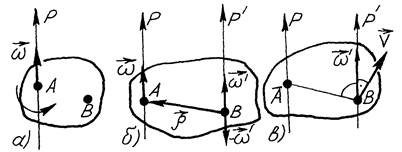
Рис. 157

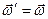В результаті в точці (рис. 157, в) залишаться вектори і 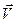, які надаватимуть точкам тіла такі ж миттєві швидкості як і вектор , що був прикладений в точці .

Отже, якщо при паралельному переносі вектора кутової швидкості в довільну точку приєднується пара обертань, момент якої геометрично рівний моменту заданої кутової швидкості відносно точки переносу, то розподіл миттєвих швидкостей в тілі не зміниться.

Отриману теорему використаємо для доведення теореми, яка за доведенням і змістом формально подібна (аналогічна) зведенню довільної системи сил до канонічного вигляду.