Найменше значення головного моменту системи сил
Для визначення найменшого значення головного моменту системи сил довільну систему сил, яка не зображена на рис. 18, послідовно зведемо до двох центрів (точок):  – довільна точка;
– довільна точка;  – точка, яка знаходиться на центральній осі системи (рис. 18).
– точка, яка знаходиться на центральній осі системи (рис. 18).
Позначимо відстань центра зведення  до центральної осі системи через
до центральної осі системи через 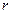 , тоді (див. § 21)
, тоді (див. § 21)
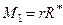 .
.
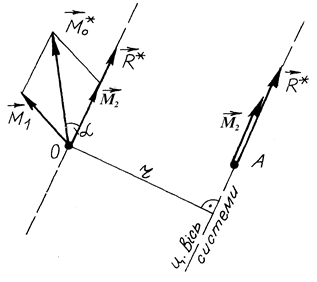
Рис. 18
Отже,
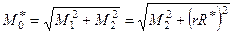 ,
,
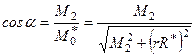 .
.
Величина головного моменту відносно будь-якої точки зведення  і кутнахилу його до головного вектора залежить від відстані даної точки до центральної осі системи. З отриманих формул можна зробити такі висновки:
і кутнахилу його до головного вектора залежить від відстані даної точки до центральної осі системи. З отриманих формул можна зробити такі висновки:
1. Для всіх центрів зведення, які знаходяться на одній і тій же відстані 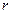 від центральної осі (тобто лежать на поверхні колового циліндра, вісь якого є центральною віссю даної системи і радіус основи якого дорівнює
від центральної осі (тобто лежать на поверхні колового циліндра, вісь якого є центральною віссю даної системи і радіус основи якого дорівнює 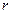 ), головний момент системи сил
), головний момент системи сил 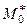 має одну і ту ж величину і утворює один і той же кут з головним вектором
має одну і ту ж величину і утворює один і той же кут з головним вектором 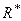 . Цим і пояснюється термін “центральна вісь системи”.
. Цим і пояснюється термін “центральна вісь системи”.
2. Величина головного моменту і його кут нахилу до головного вектора зростають разом із зростанням 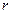 .
.
3. Головний момент має найменше значення для 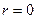 , тобто відносно точок центральної осі системи.
, тобто відносно точок центральної осі системи.
Отже, відносно точок центральної осі системи величина головного моменту має найменше значення, яке дорівнює (див. § 21) проекції головного моменту 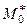 відносно довільної точки на напрям головного вектора
відносно довільної точки на напрям головного вектора
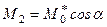 .
.
Якщо цю рівність домножити і поділити на величину головного вектора, то отримуємо формулу для обчислення найменшого значення головного моменту
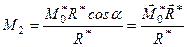 ,
,
або
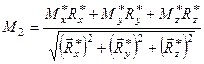 .
.
Дата добавления: 2015-06-10; просмотров: 646;
