Теорема
Сукупність одночасних “n” поступальних рухів, швидкості яких 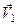 ,
, 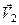 , ...,
, ..., 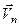 і “m” миттєвих обертальних рухів з кутовими швидкостями
і “m” миттєвих обертальних рухів з кутовими швидкостями 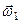 ,
, 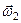 , ...,
, ...,  твердого тіла, еквівалентна сукупності одного поступального і одного обертального рухів. Кутова швидкість
твердого тіла, еквівалентна сукупності одного поступального і одного обертального рухів. Кутова швидкість  результуючого обертання дорівнює геометричній сумі (головному вектору) кутових швидкостей складових обертань
результуючого обертання дорівнює геометричній сумі (головному вектору) кутових швидкостей складових обертань
 , (2.110)
, (2.110)
а швидкість 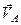 результуючого поступального руху дорівнює геометричній сумі моментів кутових швидкостей
результуючого поступального руху дорівнює геометричній сумі моментів кутових швидкостей  відносно центра зведення і швидкостей поступальних рухів
відносно центра зведення і швидкостей поступальних рухів
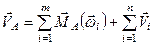 . (2.111)
. (2.111)
Оскільки кожний поступальний рух можна представити відповідною парою обертань, то геометрична сума (2.111) є не що інше, як головний момент кутових швидкостей відносно центра зведення.
Доведення сформульованої теореми з врахуванням наведених аналогій між статикою і кінематикою є дуже простим. Розглянемо тіло, яке одночасно здійснює 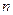 поступальних рухів з швидкостями
поступальних рухів з швидкостями 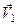 ,
, 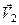 , ...,
, ..., 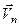 і
і 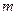 миттєвих обертальних рухів з кутовими швидкостями
миттєвих обертальних рухів з кутовими швидкостями 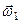 ,
, 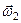 , ...,
, ...,  (рис. 158, а). Виберемо точку
(рис. 158, а). Виберемо точку  центром зведення. Враховуючи, що вектори кутових швидкостей
центром зведення. Враховуючи, що вектори кутових швидкостей  є ковзними векторами і, користуючись правилом їх паралельного переносу (див. попередню теорему), переносимо їх до центра
є ковзними векторами і, користуючись правилом їх паралельного переносу (див. попередню теорему), переносимо їх до центра  . В результаті такої
. В результаті такої
дії отримаємо сукупність векторів кутових швидкостей
( 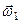 ,
, 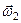 , ...,
, ...,  ), прикладених до точки
), прикладених до точки  і пар обертань, моменти яких визначають відповідні поступальні рухи
і пар обертань, моменти яких визначають відповідні поступальні рухи
 ,
, 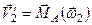 , ...,
, ..., 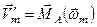 . (а)
. (а)
За правилом складання обертань навколо осей, що перетинаються, зведемо обертання з кутовими швидкостями
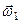 ,
, 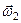 , ...,
, ...,  , які тепер прикладені до однієї точки
, які тепер прикладені до однієї точки  , до одного обертання з кутовою швидкістю, яка дорівнює геометричній сумі заданих кутових швидкостей
, до одного обертання з кутовою швидкістю, яка дорівнює геометричній сумі заданих кутових швидкостей
 . (б)
. (б)
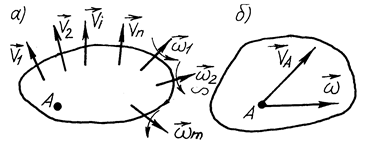
Рис. 158
Вектори швидкостей поступальних рухів 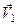 ,
, 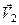 , ...,
, ..., 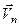 є вільними векторами, то, паралельно перенісши їх до точки
є вільними векторами, то, паралельно перенісши їх до точки  і геометрично склавши, отримаємо
і геометрично склавши, отримаємо
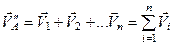 .
.
Склавши отриману швидкість  з швидкостями
з швидкостями  ,
,  , ...,
, ..., 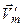 знайдемо швидкість результуючого поступального руху
знайдемо швидкість результуючого поступального руху
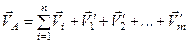 .
.
Враховуючи (а), матимемо

або
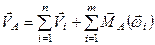 . (в)
. (в)
Отримані результати і рівності (б) і (в) підтверджують сформульовану теорему, отже вона доведена.
Розвиваючи далі аналогію між статикою і кінематикою, можна показати (читачу пропонується це проробити самостійно), що:
1. В кінематиці, як і в статиці, є два інваріанти, тобто дві величини, які не залежать від вибору центра зведення рухів. Першим інваріантом є головний вектор обертання, який визначається за формулою (2.110). Другим інваріантом є скаляр-ний добуток головного вектора обертання (формула 2.110) на головний момент (вектора швидкості результуючого поступального руху, формула (2.111)).
2. Якщо результуюча швидкість поступального руху (головний момент) дорівнює нулеві, то рух тіла, який складається з 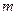 обертальних рухів і
обертальних рухів і 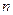 поступальних рухів, зведеться до одного обертального руху, кутова швидкість якого визначається за формулою (2.110).
поступальних рухів, зведеться до одного обертального руху, кутова швидкість якого визначається за формулою (2.110).
3. Якщо кутова швидкість результуючого обертання (головний вектор обертання) дорівнює нулеві, то рух тіла, який складається з 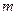 обертальних рухів і
обертальних рухів і 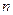 поступальних рухів, зведеться до одного поступального руху, швидкість якого визначатиметься за формулою (2.111).
поступальних рухів, зведеться до одного поступального руху, швидкість якого визначатиметься за формулою (2.111).
4. За умови  ,
,  ,
,  результуючим рухом тіла буде обертальний рух навколо осі, що буде зміщена від центра зведення
результуючим рухом тіла буде обертальний рух навколо осі, що буде зміщена від центра зведення  на відстань
на відстань 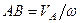 .
.
5. Якщо вектор  ,
,  і вони не є взаємно перпендикулярними, тобто їх скалярний добуток
і вони не є взаємно перпендикулярними, тобто їх скалярний добуток  , відмінний від нуля, то вся система рухів твердого тіла зведеться до кінематичного гвинта.
, відмінний від нуля, то вся система рухів твердого тіла зведеться до кінематичного гвинта.
Все перераховане аналогічне частковим випадкам зведення довільної системи сил до заданого центра (§ 21).
Д О Д А Т К И
1 Проекція вектора на площину
Проекцією вектора 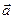 на площину є вектор
на площину є вектор 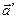 , який обмежений проекціями початку і кінця вектора
, який обмежений проекціями початку і кінця вектора 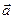 на задану площину(рис.1).
на задану площину(рис.1).

Рис. 1
Отже, щоб знайти проекцію деякого вектора 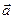 на якусь площину, наприклад, площину
на якусь площину, наприклад, площину 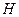 (див. рис. 1), необхідно з точки
(див. рис. 1), необхідно з точки  і
і  , які визначають початок і кінець вектора
, які визначають початок і кінець вектора 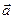 , опустити перпендикуляри
, опустити перпендикуляри 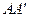 і
і  на задану площину. Основи цих перпендикулярів
на задану площину. Основи цих перпендикулярів 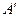 і
і 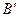 визначають проекції точок
визначають проекції точок  і
і  на площину
на площину 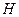 .
.
2 Проекція вектора на вісь
Проекцією вектора 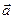 на вісь є скалярна алгебраїчна величина, яка дорівнює взятій з відповідним знаком довжині відрізка, обмеженого проекціями початку і кінця вектора
на вісь є скалярна алгебраїчна величина, яка дорівнює взятій з відповідним знаком довжині відрізка, обмеженого проекціями початку і кінця вектора 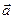 на задану вісь(рис.2).
на задану вісь(рис.2).
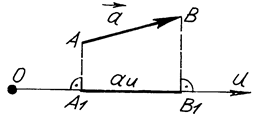
Рис. 2
Отже, щоб знайти проекцію деякого вектора 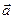 на якусь вісь, наприклад, вісь
на якусь вісь, наприклад, вісь 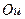 (див. рис. 2), необхідно з точок
(див. рис. 2), необхідно з точок  і
і  , які визначають початок і кінець вектора
, які визначають початок і кінець вектора 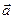 , опустити перпендикуляри
, опустити перпендикуляри  і
і 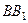 на задану вісь. Основи цих перпендикулярів (точки
на задану вісь. Основи цих перпендикулярів (точки 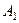 і
і 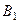 ) визначають проекції точок
) визначають проекції точок  і
і  на вісь
на вісь 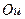 ,а відрізок
,а відрізок 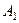
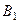 – проекцію вектора
– проекцію вектора 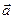 на вісь
на вісь 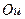 .
.
Проекція вектора на вісь найчастіше позначається тією ж літерою, що і вектор, з індексом осі на яку він проектується. В даному випадку  . Проекції вектора
. Проекції вектора 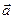 на декартові осі координат позначаються так:
на декартові осі координат позначаються так: 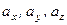 .
.
Проекція вектора на вісь вважається додатною, якщо напрям відрізка, що визначає цю проекцію, збігається з напрямом осі ( 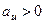 , див. рис. 2) і від’ємною – в протилежному випадку(
, див. рис. 2) і від’ємною – в протилежному випадку(  , див. рис. 3,а).
, див. рис. 3,а).

Рис. 3
Якщо позначити  кут між вектором
кут між вектором  і додатним напрямом осі, то (див. рис. 3.б), отримаємо
і додатним напрямом осі, то (див. рис. 3.б), отримаємо
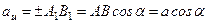 , (Д.1)
, (Д.1)
тобто,
проекція вектора на вісь дорівнює добутку модуля вектора на косинус кута між додатним напрямом осі і вектором, який проектується.
З формули (Д.1) випливає, що:
 , якщо
, якщо 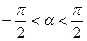 ;
;
 , якщо
, якщо  або
або 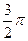 ;
;
 , якщо
, якщо  (рис. 3).
(рис. 3).
Зауваження. Якщо вектор 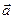 і вісь
і вісь 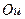 не лежать в одній площині (рис. 4), то для знаходження проекції цього вектора на вісь часто користуються подвійним проектуванням. Через вісь
не лежать в одній площині (рис. 4), то для знаходження проекції цього вектора на вісь часто користуються подвійним проектуванням. Через вісь 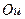 проводять довільну площину
проводять довільну площину 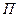 , на яку проектують вектор
, на яку проектують вектор 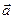 . Величина цієї проекції
. Величина цієї проекції 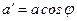 , де
, де 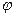 – кут між вектором
– кут між вектором 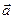 і площиною
і площиною 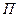 .
.

Рис. 4
Отриману проекцію 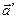 проектують на дану вісь
проектують на дану вісь 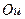 :
:  . Тут
. Тут  – кут між вектором
– кут між вектором 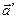 і додатним напрямом осі
і додатним напрямом осі 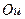 .
.
3 Приклади розв’язування задач на рівновагу тіла
Задача 3.1. Вуличний ліхтар вагою 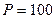 Н підвішено до вертикальної стіни за допомогою кронштейна, як вказано на рис. 5. Визначити зусилля, які виникають в стержнях крон-штейна, вважаючи їх невагомими. Кріплення в точках
Н підвішено до вертикальної стіни за допомогою кронштейна, як вказано на рис. 5. Визначити зусилля, які виникають в стержнях крон-штейна, вважаючи їх невагомими. Кріплення в точках  ,
,  і
і 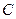 – шарнірні.
– шарнірні.
Розв’язання. Розглянемо рівновагу вузла 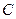 . На нього діє одна задана сила – це сила ваги ліхтаря (рис. 6). На вузол накладено дві в’язі: невагомі стрижні
. На нього діє одна задана сила – це сила ваги ліхтаря (рис. 6). На вузол накладено дві в’язі: невагомі стрижні  і
і 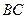 з шарнірами на кінцях. Їх реакції, як відомо (див. § 5), напрямлені вздовж цих стрижнів. Як видно з рисунка, стрижень
з шарнірами на кінцях. Їх реакції, як відомо (див. § 5), напрямлені вздовж цих стрижнів. Як видно з рисунка, стрижень  працює на розтяг, тому його реакція
працює на розтяг, тому його реакція  напрямлена від вузла
напрямлена від вузла 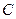 . Стрижень
. Стрижень 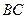 працює на стиск, і його реакція
працює на стиск, і його реакція  напрямлена до вузла. Отже, сили, що діють на вузол
напрямлена до вузла. Отже, сили, що діють на вузол 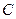 , утворюють плоску систему збіжних сил і до неї можна застосувати як геометричну, так і аналітичну умови рівноваги (див. § 8).
, утворюють плоску систему збіжних сил і до неї можна застосувати як геометричну, так і аналітичну умови рівноваги (див. § 8).
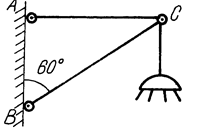 Рис. 5
Рис. 5
| 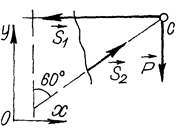 Рис. 6
Рис. 6
|
Геометрична система рівноваги – це замкнутий силовий багатокутник. Для побудови його з точки  , що береться поза основним рисунком, в певному масштабі відкладаємо відому силу
, що береться поза основним рисунком, в певному масштабі відкладаємо відому силу 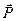 (
(  , рис. 7). З початку і кінця сили
, рис. 7). З початку і кінця сили 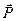 проводимо промені, які паралельні стрижням (наприклад,
проводимо промені, які паралельні стрижням (наприклад, 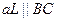 ,
, 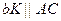 ). Точку перетину цих променів позначимо буквою
). Точку перетину цих променів позначимо буквою 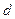 . Оскільки одержаний силовий трикутник повинен бути замкнутим, то вектори
. Оскільки одержаний силовий трикутник повинен бути замкнутим, то вектори  і
і  визначають реакції відповідних стрижнів на шарнір
визначають реакції відповідних стрижнів на шарнір 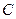 . Зазначимо, що силовий трикутник можна було б побудувати так, як вказано на рис. 8. Оскільки побудову виконано в певному масштабі, то, замірявши сторони трикутника, знаходимо величини відповідних реакцій. Згідно з рис. 7 маємо
. Зазначимо, що силовий трикутник можна було б побудувати так, як вказано на рис. 8. Оскільки побудову виконано в певному масштабі, то, замірявши сторони трикутника, знаходимо величини відповідних реакцій. Згідно з рис. 7 маємо
 ,
, 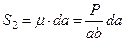 .
.
 Рис. 7
Рис. 7
|  Рис. 8
Рис. 8
|
Часто, для одержання більшої точності, побудований силовий трикутник розв’язують аналітично. Так, в даному випадку силовий трикутник є прямокутним, в якому  (рис. 7 і 8), тоді за теоремою синусів маємо
(рис. 7 і 8), тоді за теоремою синусів маємо
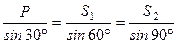 ,
,
звідси
 ,
,  .
.
Для аналітичного розв’язку задачі необхідно скласти рівняння рівноваги плоскої системи збіжних сил.
В нашому випадку (див. рис. 6, на якому вказано вибрану систему координат) маємо
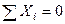
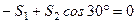 ,
,
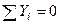
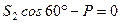 .
.
Звідси отримаємо
 ,
,
 ,
,
що узгоджується з попереднім.
Задача 3.2. Вантаж вагою  висить на тросі, який перекинуто через блок
висить на тросі, який перекинуто через блок  і напрямлено до коловорота
і напрямлено до коловорота 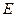 (рис. 9). Нехтуючи тертям на блоці і вагою стрижнів, визначити зусилля в стрижнях
(рис. 9). Нехтуючи тертям на блоці і вагою стрижнів, визначити зусилля в стрижнях 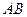 ,
, 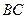 і
і 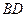 , які підтримують блок
, які підтримують блок  , вважаючи їх кріплення шарнірними.
, вважаючи їх кріплення шарнірними.

Рис. 9
Розв’язання. Розглянемо рівновагу блока  . На нього діють (рис. 10):
. На нього діють (рис. 10):
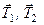 – натяги частин
– натяги частин  і
і 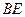 троса, які, очевидно, є рівними між собою і чисельно дорівнюють вазі вантажу, тобто
троса, які, очевидно, є рівними між собою і чисельно дорівнюють вазі вантажу, тобто
 ;
;

Рис. 10
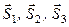 – реакції невагомих стрижнів з шарнірами на кінцях. Ці реакції напрямлені вздовж прямих
– реакції невагомих стрижнів з шарнірами на кінцях. Ці реакції напрямлені вздовж прямих 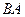 ,
, 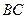 і
і 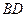 і дорівнюють шуканим зусиллям в стрижнях. До того ж, вважаючи, що всі стрижні працюють на розтяг, реакції їх напрямляємо від вузла
і дорівнюють шуканим зусиллям в стрижнях. До того ж, вважаючи, що всі стрижні працюють на розтяг, реакції їх напрямляємо від вузла  .
.
Отримана система сил є просторовою збіжною. Складаємо її рівняння рівноваги
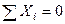
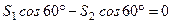 ;
;
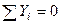
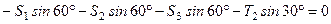 ;
;
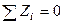
 .
.
Звідси знаходимо
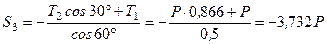
 .
.
Оскільки 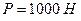 , то остаточно отримаємо
, то остаточно отримаємо
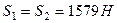 ,
,
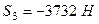 .
.
Знак мінус біля значення 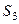 вказує на те, що відповідний стрижень, в даному випадку стрижень
вказує на те, що відповідний стрижень, в даному випадку стрижень 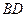 , працює на стиск.
, працює на стиск.
Задача 3.3. Знайти реакції жорсткого защемлення балки 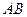 , яка завантажена на відрізку
, яка завантажена на відрізку 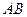 рівномірно розподіленим навантаженням інтенсивності
рівномірно розподіленим навантаженням інтенсивності 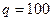 Н/м, в точці
Н/м, в точці 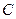 зосередженою силою
зосередженою силою  кН під кутом
кН під кутом  до балки і парою сил з моментом
до балки і парою сил з моментом  кН×м. Розміри вказані на рис. 11.
кН×м. Розміри вказані на рис. 11.
Розв’язання. За об’єкт рівноваги вибираємо балку  . Активними силами, прикладеними до балки, будуть: сила
. Активними силами, прикладеними до балки, будуть: сила  ; пара сил з моментом
; пара сил з моментом 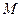 ; рівномірно розподілене навантаження
; рівномірно розподілене навантаження 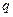 , рівнодійна якого дорівнює
, рівнодійна якого дорівнює
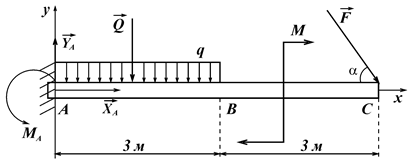
Рис. 11
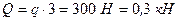 .
.
В’яззю, накладеною на балку, є жорстке защемлення  . Заміняємо дію цієї в’язі реакціями
. Заміняємо дію цієї в’язі реакціями  і реактивним моментом
і реактивним моментом  .
.
На балку 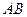 діє плоска довільна система сил. Рівняння рівноваги
діє плоска довільна система сил. Рівняння рівноваги
 ;
;
 ;
;
 .
.
Розв’язуючи цю систему рівнянь, отримаємо
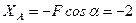 кН ,
кН ,
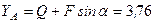 кН ,
кН ,
 кН×м .
кН×м .
Задача 3.4. Плита 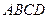 вагою
вагою 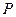 утримується в горизонтальному положенні за допомогою сферичного шарніра
утримується в горизонтальному положенні за допомогою сферичного шарніра  , завіси
, завіси  і невагомого стрижня
і невагомого стрижня 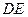 , розміщеного в площині, паралельній координатній площині
, розміщеного в площині, паралельній координатній площині 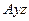 (рис. 12). У площині плити діє пара сил з моментом
(рис. 12). У площині плити діє пара сил з моментом 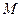 . Визначити реакції опор і зусилля в стрижні
. Визначити реакції опор і зусилля в стрижні 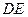 , якщо
, якщо  кН,
кН,  кН,
кН,  м,
м,  м,
м, 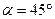 .
.
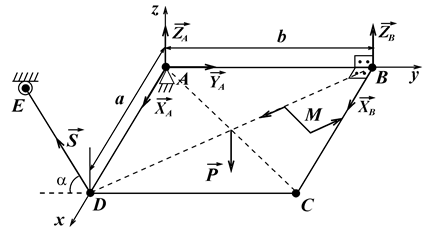
Рис. 12
Розв’язання. Об’єкт рівноваги – плита. Активна сила 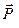 , пара сил з моментом
, пара сил з моментом 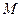 , реакції в’язей
, реакції в’язей 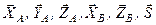 показані на рис. 12. На плиту діє довільна просторова система сил, для якої запишемо рівняння рівноваги
показані на рис. 12. На плиту діє довільна просторова система сил, для якої запишемо рівняння рівноваги
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Розв’язуючи отриману систему рівнянь знаходимо невідомі реакції

 ;
;
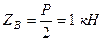 ;
;  ;
;
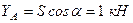 ;
;  .
.
Дата добавления: 2015-06-10; просмотров: 966;
