Тертя ковзання

Опір, що виникає при ковзанні або намаганні ковзати одного тіла по поверхні іншого, називається тертям ковзання.

Розглянемо тіло Д, що знаходиться на горизонтальній поверхні. Позначимо (рис. 60, а) – силу ваги тіла; – нор-мальну реакцію поверхні.

Прикладемо до тіла горизонтальну силу 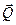(рис. 60, б). Якщо б реакція поверхні визначалась тільки однією силою , то під дією незначного зусилля 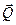тіло ковзало б по повер-хні. В дійсності цього не спостерігається. Як показує практика, інколи треба прикласти значне зусилля, щоб змусити тіло ковзати по по-верхні. Отже, між повер-хнею і тілом виникає сила, яка протидіє ковзанню тіла по поверхні і зрівноважує силу 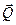. Ця сила називається силою тертя – статичною силою тертя, бо тіло перебуває в стані спокою (або силою зчеплення) і позначається (рис. 60, в).

З умови рівноваги ( 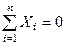) маємо

,

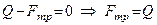тобто, при рівновазі тіла сила тертя дорівнює силі, яка намагається сунути тіло по поверхні. Отже, 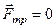, якщо 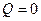. Для 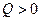сила тертя також більша від нуля .

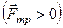Експериментальними дослідженнями Леонардо да Вінчі (1508 р.), французького механіка Г.Амонтона і французького фізика Ш.Кулона (1781 р.) для сили тертя були встановлені такі закони (закони Амонтона-Кулона):

1. Сила тертя знаходиться в спільній дотичній площині до поверхонь тіл, які стикаються, і напрямлена в бік, протилежний напряму можливого ковзання тіла під дією активних сил. Величина сили тертя залежить від активних сил і змінюється від нуля до свого максимального значення, яке вона набуває в момент виходу тіла з рівноважного стану, тобто

.

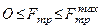2. Максимальна сила тертя пропорційна нормальному тиску тіла на поверхню

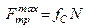, (1.59)

де безрозмірний коефіцієнт 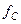називається коефіцієнтом тертя (коефіцієнтом статичного тертя).

3. Максимальна сила тертя при інших однакових умовах не залежить від площі контакту тіла з поверхнею. З цього закону випливає, що для того, щоб зсунути тіло форми паралелепіпеда (наприклад, цеглу), треба прикласти одну і ту ж силу незалежно від того, якою гранню (широкою або вузькою) він лежить на поверхні.

4. Коефіцієнт тертя залежить від матеріалу тіл, що контактують. Так, коефіцієнт тертя сталі по сталі дорівнює 0,15, сірого чавуну по сірому чавуну – 0,22, бронзи по залізу – 0,19, шкіри по чавуну – 0,28 і т.ін.

5. Коефіцієнт тертя залежить від фізичного стану поверхонь тіл , що контактують, тобто від величини і характеру їх шорсткості, вологості, температури і т.ін. З підвищенням температури коефіцієнт тертя здебільшого зростає.

6. При ковзанні тіла по поверхні сила тертя напрямлена в бік, протилежний напряму ковзання, і дорівнює добутку коефіцієнта тертя ковзання на нормальний тиск

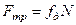, (1.60)

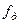– коефіцієнт тертя ковзання (динамічний коефіцієнт тертя).

Пізніше було встановлено, що:

7. Коефіцієнт тертя ковзання залежить від відносної швидкості ковзання. Для більшості матеріалів ця залежність зображена на рис. 61, з якої видно, що коефіцієнт тертя ковзання під час руху є меншим від коефіцієнта статичного тертя ( 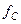). В технічних розрахунках найчастіше вважають, що коефіцієнт тертя ковзання не залежить від відносної швидкості і його приймають рівним 0,9 .

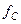Сформульовані закони про тертя ковзання відносяться тільки до сухого тертя. При наявності мастила (рідке, в’язке тертя) існують свої закони тертя, які вивчає гідромеханіка.

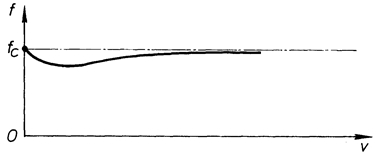
Рис. 61

§ 28 Конус тертя. Область рівноваги

Нормальна реакція і сила тертя в сумі визначають повну реакцію опорної поверхні (рис. 62), тобто реакція шорсткої поверхні дорівнює геометричній сумі вказаних сил

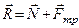. (1.61)

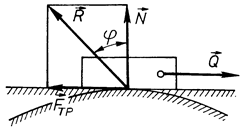
Рис. 62

Ця реакція відхилена від нормалі до поверхні на деякий кут 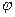. Із зміною сили тертя від нуля до максимального значення ( 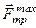) змінюватиметься і реакція поверхні від до 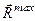, а її кут з нормаллю до поверхні збільшуватиметься від нуля до деякого граничного значення 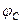(рис. 63).

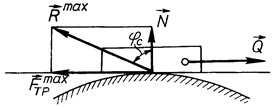
Рис. 63

Найбільший кут j_С , на який повна реакція поверхні відхиляється від нормалі до неї, називається кутом тертя.

З рис. 63 видно, що

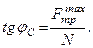
Враховуючи формулу (1.59), отримаємо

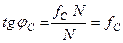, (1.62)

тобто,

тангенс кута тертя чисельно дорівнює коефіцієнту статичного тертя.

При зміні напряму прикладання активної сили 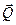буде змінюватись напрям сили тертя 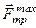, а реакція 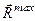поверхні буде описувати конічну поверхню (рис. 64).

Конус, вершина якого знаходиться в точці дотику тіла з поверхнею, а твірна з нормаллю до поверхні утворює кут тертя, називається конусом тертя.

Якщо коефіцієнт тертя в усіх напрямах однаковий, то конус тертя буде круговим.

Область, обмежена конусом тертя, називається обла-стю рівноваги.

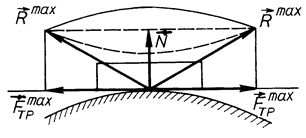
Рис. 64

Така назва пояснюється тим, що коли активні сили, котрі діють на тіло, зводяться до рівнодійної, лінія дії якої знаходиться в області, обмеженій конусом тертя, то якою б великою вона не була, тіло перебуватиме в стані спокою.

Для доведення цього розглянемо тіло на шорсткій поверхні. Позначимо рівнодійну активних сил, що діють на тіло, 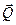і нехай вона утворює кут 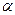з нормаллю до поверхні (рис. 65).

Умовою спокою тіла на поверхні є

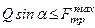, (а)

Оскільки 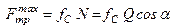, то умова (а) набуває вигляду

,

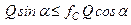або

.

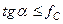Враховуючи формулу (1.62), отримуємо

.

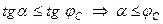З отриманої нерівності випливає, що, коли до тіла, що знаходиться на шорсткій поверхні, прикладено силу 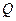, котра утворює з нормаллю до поверхні кут, менший від кута тертя, то тіло буде перебувати в стані спокою. Цим пояснюються такі відомі явища в техніці, як заклинювання або самогальмування.