Теорема. Дія пари сил, які лежать в площинах, що перетина-ються, еквівалентні одній парі сил, момент якої до-рівнює геометричній сумі моментів заданих пар сил.

Дія пари сил, які лежать в площинах, що перетина-ються, еквівалентні одній парі сил, момент якої до-рівнює геометричній сумі моментів заданих пар сил.

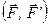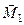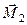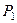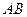Доведення. Припустимо, що задано дві пари сил і з моментами відповідно і . Пари сил лежать в площинах і , що перетинаються. – лінія перетину цих площин (рис. 36, а).

На основі теорем про еквівалентність пар приведемо задані пари сил до одного плеча 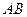(рис. 36, б). В результаті такого приведення в точках 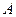і 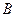буде прикладено по дві сили:

Рис. 36

в точц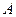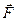і — і , в точц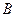і — і . Геометрично складемо ці сили

; .

Оскільки 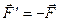і розглядаються як сили, що утворюють пари сил, то і 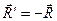. Отже, отримані сили утворюють пару сил. Таким чином, дві пари сил замінено однією парою, яка, очевидно, є еквівалентною заданим парам, бо всі перетворення, в результаті яких вона отримана, пророблені на основі теорем про еквівалентність пар і аксіоми паралелограма сил.

Визначимо момент 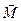отриманої пари за формулою

.

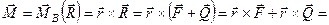
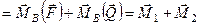Отже,

момент еквівалентної пари дорівнює геометричній сумі моментів заданих пар

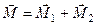. (1.37)

Розглянемо систему пар сил з моментами відповідно 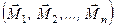. Склавши перші дві пари, отримаємо пару сил, еквівалентну їм, з моментом

.

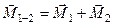Одержану пару сил складемо з третьою і отримаємо пару сил, яка вже буде еквівалентна трьом парам сил. Її момент

.

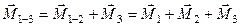Продовживши додавання і виконавши складання, отри-маємо одну пару сил з моментом

,

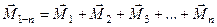яка буде еквівалентною заданій системі пар сил.

Отже,

дію на тверде тіло системи пар сил, довільно розміщених в просторі, можна замінити дією однієї пари сил, момент якої дорівнює геометричній сумі моментів всіх пар системи

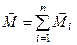. (1.38)

Іншими словами, канонічним виглядом системи пар сил є пара сил з моментом 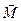, який визначається за формулою (1.38).

Якщо момент результуючої пари буде дорівнювати нулеві, то це означає, що дія системи пар сил на тверде тіло рівна нулеві, тобто система пар сил є зрівноваженою.

Таким чином,

система пар сил, які розміщені довільно в просторі, знаходиться в рівновазі, якщо геометрична сума мо-ментів всіх пар, що утворюють систему, дорівнює нулеві

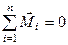. (1.39)

Рівність (1.39) є необхідною і достатньою умовою рівноваги системи пар сил.

Спроектувавши векторну рівність (1.39) на координатні осі і пам’ятаючи, що проекція векторної суми на вісь дорівнює алгебраїчній сумі відповідних проекцій, отримаємо

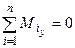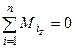; ; . (1.40)

Це аналітичні умови рівноваги системи пар сил, які формулюються так:

для рівноваги системи пар сил, які довільно розміщені в просторі, необхідно і достатньо, щоб алгебраїчні суми проекцій її моментів на три координатні осі відповідно дорівнювали нулеві.

В частковому випадку, коли системи пар сил розміщені в одній площині, а це означає, що їх вектори моментів паралельні між собою, рівності (1.38) і (1.39) набувають такого значення:

момент пари сил, яка еквівалентна системі пар, розміщених в одній площині, дорівнює сумі алгебраїчних моментів складових пар

; (1.41)

система пар сил, розміщених в одній площині, знаходиться в рівновазі, якщо сума їх алгебраїчних мо-ментів дорівнює нулеві

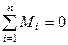. (1.42)