Теорема. Для того чтобы функция W = f(Z) имела в точке конечную производную , необходимо и достаточно, чтобы ее действительная и мнимая части u =u (x,y)
Для того чтобы функция W = f(Z) имела в точке  конечную производную
конечную производную 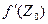 , необходимо и достаточно, чтобы ее действительная и мнимая части u =u (x,y), v = v(x,y), были дифференцируемы соответственно в
, необходимо и достаточно, чтобы ее действительная и мнимая части u =u (x,y), v = v(x,y), были дифференцируемы соответственно в 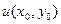 и
и  , и чтобы в этой точке (
, и чтобы в этой точке (  ) выполнялись равенства
) выполнялись равенства
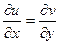 ;
;  (2),
(2),
(Коши-Римана, правильнее Даламбера-Эйлера).
Доказательство.
Необходимость. Пусть функция W = f(Z) имеет в точке Z0 конечную производную 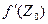 . Покажем, что функции u = u(x,y) и v = v(x,y) дифференцируемы в точке (
. Покажем, что функции u = u(x,y) и v = v(x,y) дифференцируемы в точке (  ), и что в этой точке выполняются равенства (2).
), и что в этой точке выполняются равенства (2).
В силу существования производной 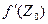 имеет место представление
имеет место представление  (3), в котором величина
(3), в котором величина 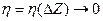 при
при 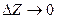 .
.
Введем обозначения:  ,
, 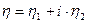 , где
, где  и
и  зависят от
зависят от  и
и  и стремятся к нулю тогда, когда одновременно стремятся к нулю
и стремятся к нулю тогда, когда одновременно стремятся к нулю  и
и  . Таким образом, можно написать, что
. Таким образом, можно написать, что 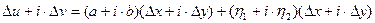 . Приравнивая здесь действительные и мнимые части. мы получаем, что
. Приравнивая здесь действительные и мнимые части. мы получаем, что
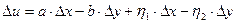 (4)
(4)
 (5).
(5).
Так как  при
при  , то из (4), (5) следует, что функции u и v дифференцируемы в u(
, то из (4), (5) следует, что функции u и v дифференцируемы в u(  ), при этом в точке (
), при этом в точке (  )
) 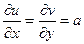 ,
,  , следовательно, выполняется условие Коши-Римана. Необходимость доказана.
, следовательно, выполняется условие Коши-Римана. Необходимость доказана.
Достаточность. Пусть вещественная и мнимая части u и v функции f(Z) дифференцируемы в точке (  ), и в этой точке выполняются равенства (2), покажем, что функция f(Z) имеет в точке
), и в этой точке выполняются равенства (2), покажем, что функция f(Z) имеет в точке  конечную производную.
конечную производную.
Введем обозначения. Пусть значения частных производных  ,
,  ,
, 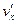 ,
, 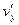 в точке (
в точке (  ) соответственно равны
) соответственно равны 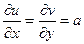 ,
,  (так как выполняются равенства (2)). Тогда в силу дифференцируемости функции u и v в точке (
(так как выполняются равенства (2)). Тогда в силу дифференцируемости функции u и v в точке (  ) в этой точке будут иметь место представления
) в этой точке будут иметь место представления
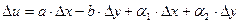
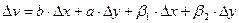 ,
,
где величины 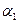 ,
,  ,
, 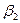 ,
,  , зависящие от
, зависящие от  и
и  , стремятся к нулю, когда одновременно
, стремятся к нулю, когда одновременно  .
.
Таким образом,
 Очевидно, модуль
Очевидно, модуль  (
(  ). Так правая часть последнего неравенства стремится к нулю при одновременном стремлении к нулю
). Так правая часть последнего неравенства стремится к нулю при одновременном стремлении к нулю  и
и  , то величина
, то величина 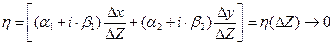 , когда
, когда 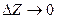 .
.
Таким образом, в точке  имеет место представление
имеет место представление  , где
, где 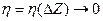 ,
, 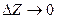 , значит функция W=f(Z) дифференцируема в точке Z0 и ее производная
, значит функция W=f(Z) дифференцируема в точке Z0 и ее производная  . Достаточность установлена.
. Достаточность установлена.
Так как функции  ,
,  являются непрерывно дифференцируемыми функциями, то сложные функции
являются непрерывно дифференцируемыми функциями, то сложные функции 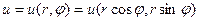 и
и 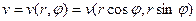 также являются дифференцируемыми в точке (
также являются дифференцируемыми в точке ( 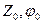 ).
).
Покажем, что в точке ( 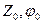 ) выполняется условие (1).
) выполняется условие (1).
Очевидно, 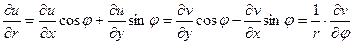
(так как  ) и
) и
 .
.
Дата добавления: 2015-06-12; просмотров: 895;
