Примеры. Проверить условие Коши-Римана для функции
Проверить условие Коши-Римана для функции
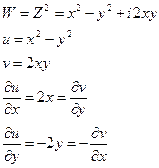
Проверить условие Коши-Римана для функции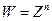 
( 
).
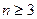Очевидно в полярных координатах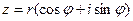 
. Поэтому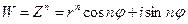 
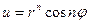
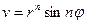
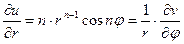(выполняется)
.
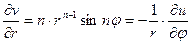Итак, эта функция является аналитической.
Отметим, что в полярных координатах производная комплексной функции вычисляется по формулам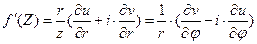 
, где 
.
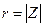Дата добавления: 2015-06-12; просмотров: 1260;