Конформные отображения

Отображение, осуществляемое посредством непрерывной функции W = f(Z), называется конформным в точке Z₀, если оно сохраняет углы между кривыми, выходящими из точки Z₀.

Если при этом отображении сохраняется не только величина угла между кривыми, но и направление отсчета, то говорят о конформном отображении 1^го рода.

Если же при отображении W = f(Z) величина углов между кривыми сохраняется, а направление их отсчета меняется на противоположное, то говорят о конформном отображении 2^го рода.

Из геометрического смысла аргумента производной непосредственно следует, что аналитические функции W = f(Z) в точках Z₀, где 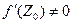, осуществляют конформное отображение 1^го рода.

Покажем, что функции, сопряженные аналитическим, осуществляют конформные отображения 2^го рода.

Рассмотрим функцию , из чертежа непосредственно видно, что функция осуществляет конформное отображение 2^го рода в любой точке .

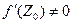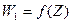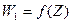Рассмотрим аналитическую функцию f(Z), которая в точке Z₀ имеет производную . Построим отображение , покажем, что оно в точке Z₀ конформное отображение 2^го рода. Очевидно, отображение представляется в виде произведения двух отображений ; . Как мы знаем, функция осуществляет в точке Z₀ конформное отображение 1^го рода. Возьмем в плоскости (Z) две кривые, исходящие из точки Z₀ и составляющие между собой угол Q.

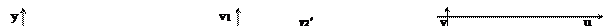
При отображении 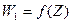эти кривые перейдут в кривые 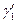и , которые также будут образовывать между собой угол Q, причем направление отсчета углов сохраняется. Произведем теперь отображение . Оно является конформным 2^го рода. Поэтому кривые 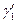и перейдут в кривые и 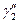, угол между которыми в точке сохраняются, но направление изменится на противоположное. Следовательно, отображение переведет кривые 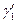, в кривые , , 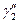угол между которыми сохраняется, но направление изменяется на противоположное. Следовательно, отображение конформное 2^го рода.