Неподвижные точки дробно-линейного отображения

Очевидно, у тождественного отображения 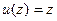все точки являются неподвижными. Будем рассматривать дробно-линейное отображение 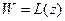с , .

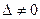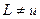Рассмотрим случай, когда 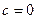. Тогда отображение W имеет вид 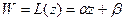, где 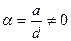, 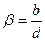. Очевидно 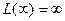. Поэтому 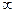является неподвижной точкой отображения L.

Если 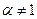, то есть еще одна неподвижная точка 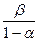( 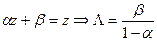). В этом случае L имеет две неподвижные точк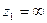и и 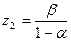. В случае, когда 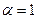, 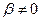других неподвижных точек, отличных от 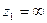нет. Однако если мы будем считать 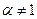и стремящиеся к единице ( 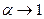), то точка 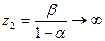. Следовательно, в случае 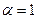, 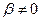бесконечность мы можем рассматривать как пару слившихся неподвижных точек.

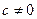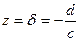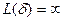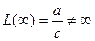Пусть теперь . Тогда в точке , , а . Следовательно, в этом случае точк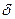и и 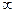не являются неподвижными. Будем считать, что 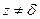, 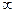. Найдем неподвижные точки отображения L, то есть такие, что 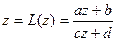; 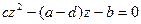. Найдем корни этого уравнения. Очевидно 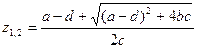. Если 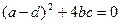, то получается кратный корень. Если же отличен от нуля, то получается два различных корня. Таким образом, и в этом случае дробно-линейная функция имеет две неподвижные точки, которые могут сливаться в одну.

Итак, всякая дробно-линейная функция 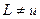с 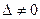имеет только две неподвижные точки, которые могут сливаться в одну точку. Следовательно, если некоторое дробно-линейное отображение имеет три неподвижные точки, то оно тождественное. Отсюда следует, что если некоторые два отображения L и 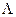имеют в трех различных точках 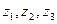одинаковые значения, то они совпадают ( ).

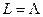В самом деле, пусть 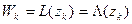(к=1, 2, 3.). Тогда обратное отображение 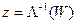будет обладать свойством 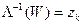(к=1, 2, 3.). Следовательно, отображение 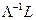будет иметь своими неподвижными точками три точки 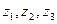: 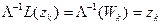. Следовательно, будет 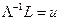одна неподвижная точка. Применяя к обеим частям равенства отображение 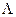, получаем (умножим обе части на 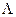, получим) 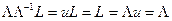. Равенство установлено.