Доказательство. Как мы знаем, существует единая дробно-линейная функция W = h(z), которая отображает точки z1, z2, z3

Как мы знаем, существует единая дробно-линейная функция W = h(z), которая отображает точки z₁, z₂, z₃, соответственно в точки W₁, W₂, W₃. Эта функция определяется из отношения:

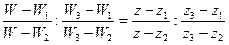(1)

(разрешим отношение W и получим необходимую функцию). Эта дробно-линейная функция отобразит прямую или окружность γ на прямую или окружность .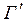

Т.к. точки z₁, z₂, z₃ 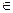γ, то точки W₁, W₂, W₃ будут принадлежать 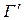. Но по построению отображения W = h(z) точки W₁, W₂, W₃ принадлежат еще Г.

Т.к. через закон различные точки W₁, W₂, W₃ можно провести через прямую или окружность, то 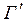= Г.

Теорема.

Пусть области g и G ограничены соответственно линиями γ и Г, каждая из которых является прямолинейной окружностью.

И тройки z₁, z₂, z₃; W₁, W₂, W₃ принадлежащие соответственно линиям γ и Г обладают свойством: при движении наблюдателя вдоль линии γ из z₁ в z₃ через z₂, которая остается слева от наблюдателя, и аналогично при движении наблюдателя вдоль линии Г из W₁ в W₃ через W₂. Область G также остается слева от наблюдателя, тогда дробно-линейная функция W=h(z), обладающая свойством: h(z_k) = W_k (k = 1, 2, 3), отображает область g на область G.