Доказательство. 1. Пусть , тогда в силу (2) будет также ( ).

1. Пусть 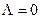, тогда в силу (2) будет также ( ).

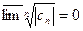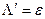Поэтому для любой фиксированной точки Z будет 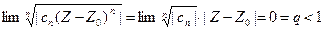, следовательно, по признаку Коши ряд (1) абсолютно сходится в любой точке Z.

2. Пусть теперь 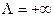. Покажем, что ряд (1) расходится в любой точке 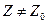. Легко видеть, что некоторая последовательность 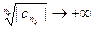. Значит для любого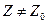 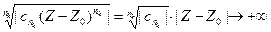и тем более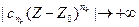

Следовательно для ряда (1) в точке 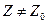не выполняется необходимый признак сходимости ряда (общий член не стремится к нулю при n→∞), поэтому ряд один в этой точке расходится.

Сходимость ряда (1) в точке Z = Z₀ очевидна, т. к. в этой точке все члены ряда (1), начиная со 2, обращаются в нуль.

3. Пусть теперь 0 < Λ < +∞. Покажем, что ряд (1) абсолютно сходится в любой точке Z круга 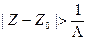. Сходимость ряда (1) в точке Z = Z₀ очевидна. Возьмем любое 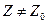из круга 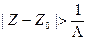. Очевидно, 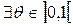такое что, будет выполняться .

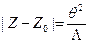Рассмотрим число 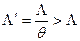. По определению верхнего предела существует число N = N( 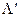), такое, что при всех n > N будет выполняться неравенство 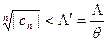. При этих номерах n > N будет .

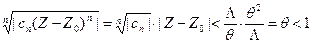Следовательно, в силу признака Коши (непредельная форма), ряд (1) в точке Z будет абсолютно сходиться.

Докажем теперь, что ряд (1) расходится в любой точке Z внешности круга .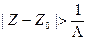

Очевидно, существует такое число 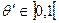, что будет выполняться равенство 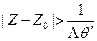. По определению верхнего предела существует подпоследовательность 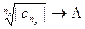, значит будет выполняться 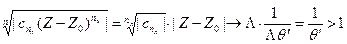, , 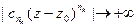поэтому в точке Z для ряда (1) не выполняется необходимое условие сходимости. Ряд в этой точке расходится.

Из теоремы Коши-Адамара вытекает. Что для любого степенного ряда (1) существует число 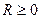, такое что, во всех числах Z круга |Z - Z₀| < R ряд (1) абсолютно сходится, а во всех точках внешности этого круга |Z - Z₀| > R ряд расходится.

Такой круг |Z - Z₀| < R называется кругом сходимости степенного ряда (1).

Число R при этом называется радиусом сходимости степенного ряда.

Очевидно,

.

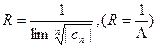Радиус окружности можно вычислить по формулам 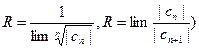, если эти пределы существуют.

Из теоремы Коши-Адамара в частности вытекает первая теорема Абеля.