Доказательство. Возьмем произвольную точку Z1 из круга |Z-Z0| < R и покажем, что во второй точке существует производная и выполняется неравенство (3)

Возьмем произвольную точку Z₁ из круга |Z-Z₀| < R и покажем, что во второй точке существует производная 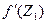и выполняется неравенство 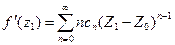(3), отсюда и будет следовать утверждение теоремы.

Вначале докажем, что ряд (2) имеет тот же ряд сходимости, что и (1) R =R'.

В самом деле,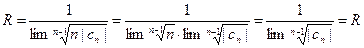

Обозначим через сумму ряда (2). Возьмем произвольную фиксированную точку G, такую, что |Z-Z₀| < |G-Z₀| = ρ < R

Очевидно для любой точки 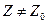из круга |Z-Z₀| < ρ имеет место равенство: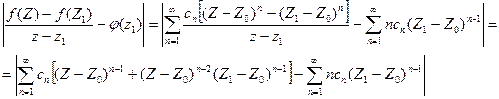

Т. к. точка G лежит внутри круга сходимости круга ряда (2), то ряд (2) в этой точке абсолютно сходится, т. е. сходится ряд.

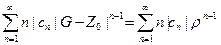(4).

Следовательно, для существует такой номер n_c = n₀(ε), такой что будет 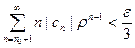(сумма остатка будет мала). Но тогда будет, 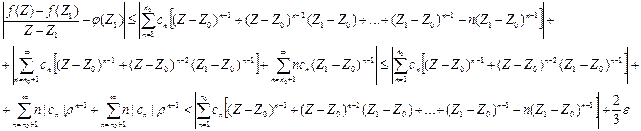Легко видеть, что функции стоящие в скобках правой части неравенства являются непрерывными функциями от Z, причем при Z = Z₁ эти функции обращаются в нуль. Поэтому для выбранного 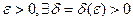, что для всех точек Z удовлетворяющих неравенству 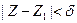будет выполняться неравенство .

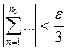Т. е. неравенство 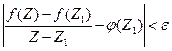выполняется, если 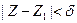, последнее означает, что .

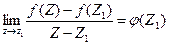Т. е. производная и равна .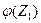

По определению - это есть сумма ряда (2). Значит

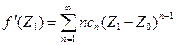
Поэтому равенство (2) выполняется для любого Z из круга |Z-Z₀| < R.

Т. к. ряд (2) имеет тот же радиус, следовательно, R > 0, то его сумма 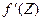тоже имеет производную в круге |Z-Z₀| < R и эта производная

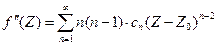
Этот процесс можно продолжать неограниченно. Поэтому мы приходим к теореме.