Доказательство. Покажем вначале, что число T = 2π∙i является периодом функции eZ, т

Покажем вначале, что число T = 2π∙i является периодом функции e^Z, т. е. что для Z выполняется равенство e^Z+2πi = e^Z. В силу теоремы сложения имеем:

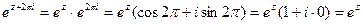
Следовательно, число T = 2πi период функции e^Z.

Покажем теперь, что это основной ее период. Возьмем произвольный период W = 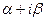функции e^Z. Будем иметь в виду, что для Z выполняется равенство: e^Z+w = e^Z. В частности, при Z = 0 получаем e^w = 1, т. е.

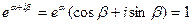
Следовательно, модули левой и правой части будут равны 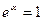и следовательно 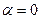. Получаем, что cosβ+isinβ = 1, т. е. cosβ = 1, sinβ = 0. Это возможно лишь в случае, когда 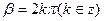, окончательно получаем, что 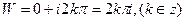. Значит, 2πi – основной период функции.