Доказательство. Мы воспользуемся следующими очевидными неравенствами:

Мы воспользуемся следующими очевидными неравенствами:

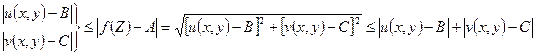(7)

Необходимость. Пусть выполняется равенство (3). Покажем, что справедливы равенства (5) и (6). Возьмем любое ε > 0, очевидно, что для него существует такое число δ > 0, что для любой точки Z принадлежащей E (Z≠Z₀), удовлетворяющее неравенству 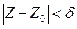, выполняется неравенство .

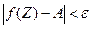Возьмем число 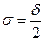, тогда для любой точки (x,y) принадлежащей E, отличной от (x₀,y₀), такой что 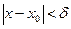, , 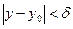будет выполняться неравенство 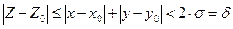и, следовательно, будет |f(Z)–A|<ε. Поэтому в силу левой части неравенств (7) будет |u(x,y)–B|<ε, |v(x,y)–C|< ε. Значит, выполняются равенства (5) и (6).

Достаточность. Пусть теперь выполняются равенства (5) и (6). Покажем, что 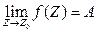(4). Возьмем любое 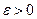, в силу (5) и (6) найдется 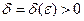, такой что, для любой точки (x,y), принадлежащей E, отличной от (x₀,y₀), удовлетворяющей неравенствам (8) 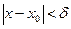, , 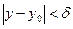будут выполняться неравенства 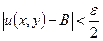, 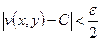(9).

Легко видеть, что для любой точки Z принадлежащей E (Z ≠ Z₀), удовлетворяющей неравенству 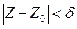, подавно будут выполняться неравенства 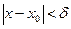, 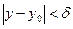. Поэтому будут выполняться неравенства (9), но тогда в силу правой части неравенств (7) для этих точек Z будет выполняться неравенство 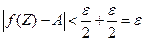. Следовательно, .

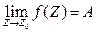Итак, существование предела комплексной функции эквивалентно существованию предела двух вещественных функций от двух переменных. Поэтому, на пределы функции комплексного переменного распространяются все основные функции пределов функции вещественной переменной. В частности справедлива теорема.