Непрерывность функции комплексного переменного

Пусть точка Z₀ принадлежащая E, является предельной точкой множества Е.

Функция f(Z) называется непрерывной в точке Z₀ принадлежащей E, если .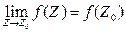

Таким образом, функция f(Z) называется непрерывной в точке Z₀ принадлежащей E, если для любого 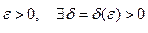, что для любой точки Z, принадлежащей E (Z ≠ Z₀), удовлетворяющей неравенству 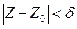, выполняется неравенство .

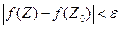Т. к. равенство 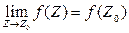эквивалентно выполнению равенств 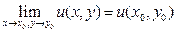, , 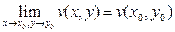то непрерывность функции f(Z) в точке Z₀ эквивалентно непрерывности вещественных функций u(x,y) и v(x,y) в соответствующей точке (x₀,y₀). Поэтому на непрерывность функции комплексного переменного распространяются все основные свойства непрерывных функций вещественных переменных. В частности справедливы теоремы.