Понятие функции комплексного переменного.
Рассмотрим в комплексной плоскости (Z) два множества E и D (не пустые).
Отображение множества 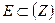 на множество
на множество 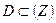 называется функцией комплексного переменного (D может принадлежать другой плоскости (W)). Любому Z0, принадлежащему E, указан каким-то способом одним элемент из D).
называется функцией комплексного переменного (D может принадлежать другой плоскости (W)). Любому Z0, принадлежащему E, указан каким-то способом одним элемент из D).
Пусть Z = x+i·y, W = u+i·v. Очевидно, что задание функции комплексного переменного эквивалентно следующему: каждой паре  (Е здесь принадлежит декартовой плоскости) ставится в соответствие два числа v и u. Следовательно, задание функции комплексного переменного W = f(Z) эквивалентно заданию вещественных функций u = u(x,y), v = v(x,y). При этом мы имеем f(Z) = u(x,y) + i·v(x,y).
(Е здесь принадлежит декартовой плоскости) ставится в соответствие два числа v и u. Следовательно, задание функции комплексного переменного W = f(Z) эквивалентно заданию вещественных функций u = u(x,y), v = v(x,y). При этом мы имеем f(Z) = u(x,y) + i·v(x,y).
Функция u(x,y) называется вещественной частью функции f(Z), а v(x,y) мнимой частью f(Z). Таким образом, Ref(Z) = u(x,y) , Imf(Z) = v(x,y).
Например, для функции W = Z2 = (x +i·y)2 = x2 – y2 + 2·i·x·y вещественная часть ReZ2 = x2 – y2, ImZ2 = 2·x·y.
Геометрически, как отображение множества 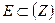 на множество
на множество 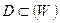 .
.
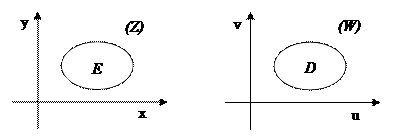
В теории аналитических функций рассматривают и многозначные функции.
Функция W = f(Z), отображающая множество 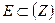 на множество
на множество 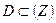 называется многозначной, если она ставит в соответствие некоторым
называется многозначной, если она ставит в соответствие некоторым  не одно, а несколько числовых значений
не одно, а несколько числовых значений 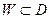 .
.
Дата добавления: 2015-06-12; просмотров: 978;
