Теорема. Из всякой бесконечной системы открытых кругов {K} накрывающей замкнутое ограниченное множество всегда можно выделить конечную подсистему кругов {K1

Из всякой бесконечной системы открытых кругов {K} накрывающей замкнутое ограниченное множество 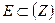всегда можно выделить конечную подсистему кругов {K₁, К₂, …, К_n}, также покрывающую множество Е.

Точка Z₀ называется внутренней точкой множества E плоскости (Z), если некоторая ее окрестность O_ε(Z₀) целиком содержится в множестве .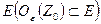

Множество E плоскости (Z), состоящее из одних внутренних точек Z, называется открытым множеством.

Множество E плоскости (Z) называется связным, если любые его две точки Z', Z'', принадлежащие E, можно соединить ломаной, целиком лежащей в множестве Е.

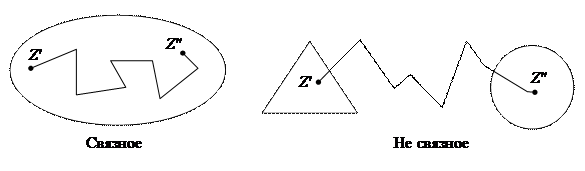
Открытое связное множество называется областью.

Пусть существует некоторое множество точек плоскости (Z). Точка Z₀ плоскости (Z) называется граничной для множества E, если в любой ее окрестность O_ε(Z₀) содержатся точки, как принадлежащие множеству E, так и не принадлежащие.

Множество всех граничных точек множества E называются границей этого множества и обозначаются Г (гамма).

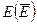Объединение (замыкание множества). Замыкание любого множества является замкнутым множеством.

Точка Z₀ принадлежащая (Z) называется внешней для множества E, если существует окрестность O_ε(Z₀), не содержащая ни одной точки из множества Е.

Очевидно, множество всех внешних точек множества E составляет отрытое множество.