Доказательство. Очевидно, нам достаточно установить, что для ряда (1) выполняются условия критерия Коши сходимости ряда

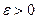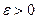
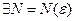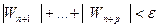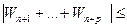
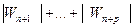Очевидно, нам достаточно установить, что для ряда (1) выполняются условия критерия Коши сходимости ряда. Возьмем любое . В силу абсолютной сходимости ряда (1), ряд (2) сходится. Поэтому для выбранного , что при любом n > N и р=1,2,… будет выполняется неравенство , но , а тем более будет выполняться неравенство 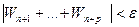при любом n > N и p=1,2,… Следовательно для ряда (1) выполняются условия критерия Коши сходимости комплексного ряда. Поэтому ряд (1) сходится. Теорема справедлива.