Ряды комплексных чисел

Символ вида W₁+W₂+…+W_n+…= 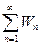(1), где W_n = u_n+i·v_n (n = 1, 2, …) комплексные числа (последовательности комплексный чисел) называются рядом комплексных чисел.

Числа W_n (n = 1, 2, …) называются членами ряда, член W_n называется общим членом ряда.

Числа вида S_n = W₁+W₂+…+W_n (2) (n = 1, 2, …), называются частичными суммами ряда (1).

Конечный или бесконечный предел S последовательности S_n называется суммой этого ряда.

Если предел S конечен, то ряд называется сходящимся, если же предел бесконечен, или вовсе не существует, то ряд расходящийся.

Если S сумма ряда (1), то пишут .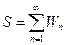

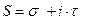Пусть , а . Очевидно σ_n=u₁+u₂+…+u_n, τ_n=v₁+v₂+…+v_n. Как мы знаем равенство 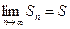(S конечно) эквивалентно двум равенствам и 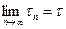. Следовательно, сходимость ряда (1) эквивалентна сходимости двух вещественных рядов: и 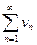. Поэтому на сходящиеся комплексные ряды распространяются основные свойства сходящихся числовых рядов.

Например, для комплексных рядов справедлив критерий Коши: ряд (1) сходится тогда и только тогда, когда для любого 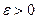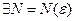, что при всех n > N и любом p = 1, 2, … выполняется неравенство .

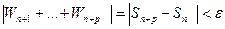Из этого критерия непосредственно следует необходимый признак сходимости ряда: для того, чтобы ряд (1) сходился необходимо и достаточно, чтобы его общий член W_n → 0.

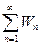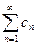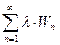Справедливы такие свойства сходящихся рядов: если ряды и сходятся к своим суммам S и d, то ряды и сходятся соответственно к суммам S ± d и λ·S .