Б) Формы записи комплексных чисел.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной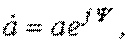

тригонометрической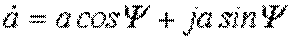

алгебраической 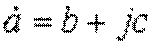формах.

Пусть дано число которое на комплексной плоскости изображено

вращающимся вектором (см. рис. 42.3)

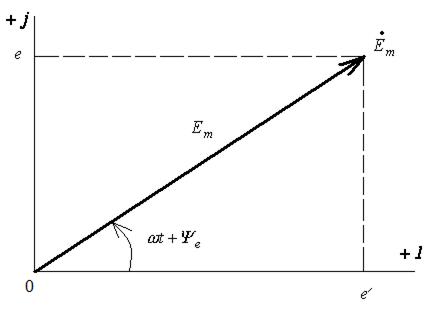
Рис.42.3. Представление числа на координатной плоскости

Тогда в показательной форме это число будет выглядеть как

в тригонометрической

в алгебраической

Модулем комплексного числа называется длина вектора OP (см. рис.42.4) , изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен

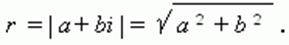
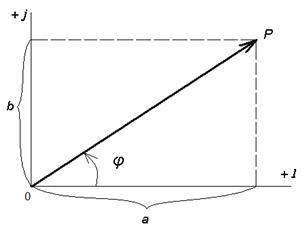
Рис.42.4. Представление комплексных чисел на плоскости

Аргумент комплексного числа - это угол φ между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tg φ = b / a .