Бесконечность и стереографическая проекция

Для нужд теории аналитических функций вводится в рассмотрение несобственное комплексное число, обозначаемое символом ∞, которое называется бесконечностью или бесконечно удаленной точкой.

Все конечные комплексные числа называются собственными. Отношение между бесконечностью и конечными комплексными числами строится на основе следующих правил и определений:

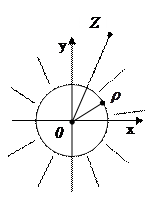
ρ-окрестностью бесконечно удаленной точки называется внешность круга, радиусом ρ с центром в нуле, т. е. множество внешних точек Z плоскости (Z), удовлетворяющих неравенству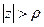

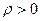
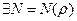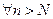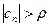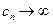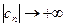Бесконечность называется пределом последовательности комплексных чисел (с_n), если для любого , что при выполнится неравенство . Таким образом, соотношения и эквивалентны.

Отметим, что по определению 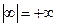, что для бесконечности не определяется вещественная и мнимая части, а так же аргумент (как и для нуля).

Пусть с произвольное конечное комплексное число, а с₀ комплексное число, не равное 0, тогда по определению 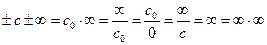, что неопределенным считается .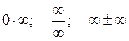

Для геометрического изображения бесконечности комплексные числа изображают точками сферы. Это делается так: около начала комплексной плоскости описывается сфера радиусом равным единице с центром в нуле. Эта сфера пересечется с комплексной плоскостью по окружности, которая называется экватором. Прямая перпендикулярная комплексной плоскости (плоскости экватора), проходящая через начало, через нуль, называется осью сферы.

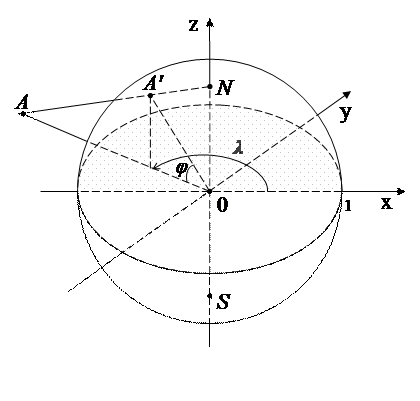
Точки встречи этой оси со сферой: N и S называются соответственно - северным и южным полюсами. Мы будем пользоваться следующими географическими понятиями: северное и южное полушария (над и под экватором), широта и долгота, меридианы и параллели. Положение любой точки A' на сфере мы будем определять заданием ее координат: широты φ и долготы λ.

Широта φ отсчитывается от плоскости экватора в пределах 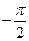до 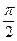. Отсчет в сторону северного полюса принимается за положительный, а в сторону южного за отрицательный.

Долгота λ отсчитывается в плоскости экватора от положительной части действительной оси 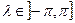, λ =ArgA .

Будем теперь соединять точки A' сферы с северным полюсом N лучами, исходящими из точки N. Точки встречи этого луча с комплексной плоскостью будем обозначать через A.

Точка A будет называться стереографической проекцией точки A' сферы. При такой проекции вся сфера проецируется на комплексную плоскость.

Точки южного полушария проецируются вовнутрь круга, а точка S в точку нуль. Южное полушарие - на единичный круг, а северное – на внешность этого круга. Этой проекцией издавна пользовались в астрономии для изображения небесного свода на плоской карте, а также в географии.

Будем теперь наоборот изображать точки A комплексной плоскости, соответствующим точкам A' сферы. Тогда каждое конечное комплексное число изображается некоторой точкой сферы A' не равной N.

Такая сфера, все точки которой являются изображением комплексных чисел, называется числовой сферой.

Пусть точка A изображает комплексное число.

c = |c|·(сos Arg с + i·sin Arg с), а A'(φ,λ). Установим связь между |c|, Arg с, φ и λ. Из чертежа непосредственно видно угол ONA = 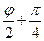(т.к. сфера единичная и угол AON = 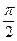), угол A'ON = 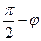, углы OA'N+ONA' = 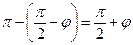, угол ONA( 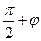)/2 = 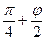, следовательно, |c| = 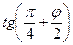и Arg с = λ. Отсюда получаем, что φ = 2·arctg|c| - 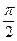, λ = arg c. Из этих равенств видно, что если 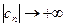, то 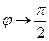, т. е. при 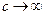, соответствующая точка A' → N. Обратно, если 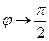, то 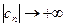, т. е. из A' → N следует, что 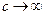, поэтому естественно принять точку N за изображение бесконечности.

Отметим, что множество всех собственных, конечных точек (Z) комплексной плоскости называется конечной комплексной плоскостью.

Если к ней мысленно присоединить бесконечно удаленную точку, то получим расширенную комплексную плоскость.

Наглядным изображением расширенной комплексной плоскости является сфера, причем N является изображением бесконечно удаленной точки. Изображением конечной комплексной плоскости является сфера, с исключенной точкой N.