Доказательство,

опирается на следующие очевидные неравенства

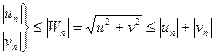(5)

Необходимость. Пусть ряд (1) абсолютно сходится, покажем, что ряд (3) и (4) абсолютно сходятся, т. е. сходятся ряды 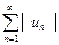и 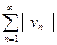(6). Из абсолютной сходимости ряда (1) следует, что ряд (2) 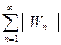сходится, тогда в силу левой части неравенства (5) ряды (6) будут сходиться, т. е. ряды (3) и (4) абсолютно сходятся.

Достаточность. Пусть ряды (3) и (4) абсолютно сходятся, покажем, что ряд (1) тоже абсолютно сходится, т. е. что сходится ряд (2). Из абсолютной сходимости рядов (3) и (4) следует, что ряды (6) сходятся, поэтому сходится и ряд 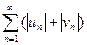. Следовательно, в силу правой части неравенства (5) ряд (2) сходится, т.е. ряд (1) абсолютно сходится.

Итак, абсолютная сходимость комплексного ряда (1) эквивалентна абсолютной сходимости вещественных числовых рядов (3) и (4). Поэтому на абсолютно сходящиеся комплексные ряды распространяются все основные свойства вещественных абсолютно сходящихся числовых рядов. В частности для абсолютно сходящегося комплексного ряда справедлива теорема о перестановке его членов, т. е. перестановка членов в абсолютно сходящемся ряде не влияет на сумму ряда. Для установления абсолютной сходимости комплексного ряда может применяться любой признак сходимости положительного ряда.