Доказательство. Мы будем доказывать теорему исходя из следующего очевидного двойного неравенства
Мы будем доказывать теорему исходя из следующего очевидного двойного неравенства
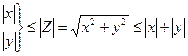 , где Z = x + y·i (2)
, где Z = x + y·i (2)
Необходимость. Пусть lim (сn) = с. Покажем, что верны равенства lim an = a и lim bn = b (3).
Очевидно 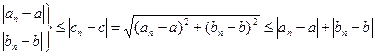 (4)
(4)
Так как 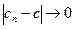 , когда n → ∞, то из левой части неравенства (4) следует, что
, когда n → ∞, то из левой части неравенства (4) следует, что 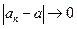 и
и 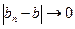 , когда n → ∞. поэтому выполняются равенства (3). Необходимость доказана.
, когда n → ∞. поэтому выполняются равенства (3). Необходимость доказана.
Достаточность. Пусть теперь выполняются равенства (3). Из равенства (3) следует, что 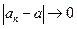 и
и 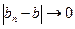 , когда n → ∞, поэтому в силу правой части неравенства (4) будет
, когда n → ∞, поэтому в силу правой части неравенства (4) будет 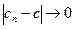 , когда n→∞, значит lim(сn)=с. Достаточность доказана.
, когда n→∞, значит lim(сn)=с. Достаточность доказана.
Итак, вопрос о сходимости последовательности комплексных чисел эквивалентен сходимости двух вещественных числовых последовательностей, поэтому на последовательности комплексных чисел распространяются все основные свойства пределов вещественных числовых последовательностей.
Например, для последовательностей комплексных чисел справедлив критерий Коши: для того, чтобы последовательность комплексных чисел (сn) сходилась, необходимо и достаточно, чтобы для любого 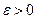
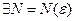 , что при любом n, m > N выполняется неравенство
, что при любом n, m > N выполняется неравенство 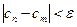 .
.
Дата добавления: 2015-06-12; просмотров: 883;
