Степень с произвольным рациональным показателем

Возьмем произвольное комплексное число с. Если n натуральное число, то сⁿ = |c|ⁿ·(сos nArg с + i·sin nArg с) (6). Эта формула верна и в случае n = 0 (с≠0) 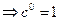. Пусть n < 0 и n 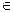Z и с ≠ 0 , тогда

сⁿ = 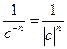(cos nArg с+i·sin nArg с) = 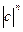(cos nArg с + i·sin nArg с). Таким образом, формула (6) справедлива для любых n.

Возьмем рациональное число 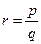, где q натуральное число, а р является целым.

Тогда под степенью c^r будем понимать число .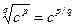

Мы получаем, что ,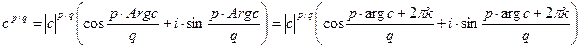

(k = 0, 1, …, q-1). Этих значений q штук, если дробь не сократима.