Затем, изымая степень, соответствующую вершине , получим

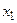
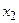
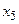
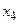
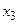
D'₁=(2, 1, 0, 1, 0).

Переупорядочивая остаточные степени в D'₁, получим

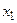
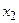
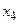
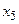
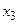
D₂=( 2, 1, 1, 0, 0).

Теперь, изымая степень, соответствующую вершине 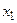, получим

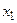
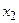
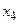
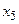
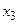
D'₂=(0, 0, 0, 0, 0).

Здесь алгоритм заканчивает работу, так как все остаточные степени равны нулю. Последовательность (4, 3, 3, 2, 2) графическая. Требуемый граф (рис. 4.22) получается в результате выполнения шагов, соответствующих порядку изъятия степеней:

1. Соединяем вершину 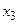с вершинам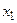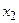и , и .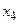

2. Соединяем вершину 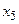с вершинам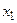и и .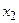

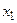3. Соединяем вершину с вершинам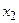и и .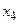

Рис. 4.22. Граф с последовательностью степеней (4, 3, 3, 2, 2)

Замечание. Можно привести пример последовательности, например, (3, 3, 1, 1), для которой условия (4.1) – (4.2) выполняются, но она не является графической. Условия (4.1) – (4.2) не являются достаточными для того, чтобы последовательность была графической.