Напряжения при вершине трещины
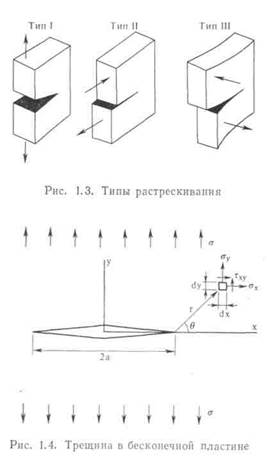 Раскрытие трещины в твердом теле может быть осуществлено тремя различными путями, как показано на рис. 1.3. При нормальных напряжениях возникает трещина типа «разрыв» (тип I): перемещения берегов трещины перпендикулярны плоскости трещины. При плоском сдвиге образуется трещина типа II, или трещина типа «сдвиг»: перемещения берегов трещины происходят в плоскости трещины и перпендикулярно ее фронтальной линии. Трещина типа «срез», или типа III, образуется при антиплоском сдвиге: перемещения берегов трещины совпадают с плоскостью трещины и параллельны ее направляющей кромке. В общем случае трещину можно описать этими тремя типами. Наиболее важное значение в технике имеет трещина типа I, обсуждением которой мы ограничимся.
Раскрытие трещины в твердом теле может быть осуществлено тремя различными путями, как показано на рис. 1.3. При нормальных напряжениях возникает трещина типа «разрыв» (тип I): перемещения берегов трещины перпендикулярны плоскости трещины. При плоском сдвиге образуется трещина типа II, или трещина типа «сдвиг»: перемещения берегов трещины происходят в плоскости трещины и перпендикулярно ее фронтальной линии. Трещина типа «срез», или типа III, образуется при антиплоском сдвиге: перемещения берегов трещины совпадают с плоскостью трещины и параллельны ее направляющей кромке. В общем случае трещину можно описать этими тремя типами. Наиболее важное значение в технике имеет трещина типа I, обсуждением которой мы ограничимся.
 Рассмотрим сквозную трещину типа I длиной 2а в бесконечной пластине, как показано на рис. 1.4. Пластина находится под действием растягивающего напряжения σ, которое вызывается приложенными в бесконечности силами. В гл. III и XIII рассмотрено несколько путей для вычисления поля упругих напряжений при'вершине трещины. Элемент dxdy пластины, расположенный на расстоянии rот вершины трещины и составляющий с плоскостью трещины угол Θ, находится под действием нормальных напряжений σχ и ау,. действующих в направлениях χ и у, и касательного напряжения τ ху-Можно показать, что эти напряжения равны :
Рассмотрим сквозную трещину типа I длиной 2а в бесконечной пластине, как показано на рис. 1.4. Пластина находится под действием растягивающего напряжения σ, которое вызывается приложенными в бесконечности силами. В гл. III и XIII рассмотрено несколько путей для вычисления поля упругих напряжений при'вершине трещины. Элемент dxdy пластины, расположенный на расстоянии rот вершины трещины и составляющий с плоскостью трещины угол Θ, находится под действием нормальных напряжений σχ и ау,. действующих в направлениях χ и у, и касательного напряжения τ ху-Можно показать, что эти напряжения равны :
В упругом случае напряжения, указанные в (1.1), пропорциональны внешнему напряжению σ. Их
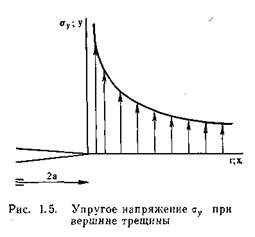 величины пропорциональны корню квадратному из размера трещины и стремятся к бесконечности в вершине трещины при обращении г в нуль. Зависимость αυ от г при 6 = 0 показана на рис. 1.5. Для больших значений г величина σ^ стремится к нулю, в то время как она должна стремиться к о. Очевидно, уравнения (1.1) справедливы только в ограниченной области — вблизи вершины трещины. Каждое из уравнений представляет собой первый член ряда. В окрестности, около вершины
величины пропорциональны корню квадратному из размера трещины и стремятся к бесконечности в вершине трещины при обращении г в нуль. Зависимость αυ от г при 6 = 0 показана на рис. 1.5. Для больших значений г величина σ^ стремится к нулю, в то время как она должна стремиться к о. Очевидно, уравнения (1.1) справедливы только в ограниченной области — вблизи вершины трещины. Каждое из уравнений представляет собой первый член ряда. В окрестности, около вершины
трещины, эти первые члены достаточно точно описывают поля напряжений, поскольку остальные члены малы по сравнению с ними. На больших расстояниях от вершины трещины следует вводить большее количество членов в уравнения (см. гл. Ill·)
В уравнениях (1.1) функции координат гиб имеют простой вид. В обобщенном в-идеэт.и ^уравнения можно записать так:
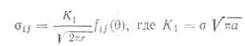
Коэффициент Κι называется коэффициентом интенсивности напряжений*, где индекс I обозначает тип I. Когда известен коэффициент, Κι, поле напряжений при вершине трещины полностью определено. Две трещины, одна размером 4а, а другая размером а, имеют одинаковые поля напряжений при их вершинах, если первая трещина нагружена напряжением σ, а вторая —напряжением 2 σ. В этом случае Κι имеет одинаковые значения для обеих трещин.
Уравнение (1.2) есть решение упругой задачи; оно не запрещает обращения напряжения при вершине трещины в бесконечность.
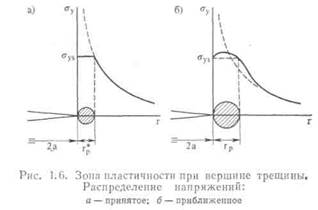
В действительности этого не может произойти: пластические деформации, возникающие при вершине трещины, ограничивают напряжения. Точное решение упругой задачи для поля напряжений еще не получено. Размер зоны пастичности при вершине трещины можно оценить, если определить расстояние от вершины трещины г*р, на котором упругое напряжение σу превышает предел текучести σ ys (рис. 1.6, а) (см. [7,8]). Подставляя σ = σ уз в уравнение (1.1) для σ у и полагая Θ = 0, получим
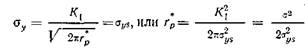
На самом деле зона пластичности несколько больше (рис. 1.6, б). Общие выражения для размера зоны пластичности рассмотрены в гл. V. Здесь достаточно отметить, что rv* можно непосредственно определить
* Отметим, что Κι отличается от коэффициента концентрации напряжений k( как по размерности, так и по смыслу. Последний представляет собой отношение максимального напряжения к номинальному в образце с выточкой.
выразить как функцию коэффициента интенсивности напряжении К1с ипредела текучести.
Выше утверждалось, что в зоне упругости трещины различных размеров, но с одинаковыми Κι, имеют одинаковые поля напряжений. Возникает вопрос: справедливо ли это утверждение в случае, когда материал испытывает пластические деформации? Согласно уравнению (1.3), трещины, нагруженные до одинаковых значений Κι, имеют зоны пластичности одинаковых размеров. Вне зоны пластичности поля напряжений будут одинаковыми. Если две трещины имеют одинаковые пластические зоны и одинаковые напряжения на границе этой зоны, то напряжения и деформации внутри зоны пластичности должны быть равными.
Иными словами, поле напряжений определяется коэффициентом интенсивности напряжений. Этим коэффициентом определяется также то, что происходит внутри зоны пластичности. Κι есть мера всех напряжений и деформаций. Когда напряжения и деформации при вершине трещины достигают критических значений, происходит расширение трещины. Это означает, что при достижении Κι критического значения Kic произойдет разрушение. Можно предполагать, что Kic есть константа материала.
Возьмем пластину с трещиной известного размера и растянем ее в испытательной машине вплоть до разрушения. По величине нагрузки, при которой произошло разрушение, можно вычислить разрушающее напряжение ас. Отсюда, зная ос, можно найти критическое значение коэффициента интенсивности напряжений в момент разрушения:
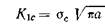
Если Kic — константа материала, то такое же значение должно быть получено при испытании образца с трещиной иного размера. В определенных пределах это действительно имеет место. Зная величину Kic, можно рассчитать прочность такого же материала с трещинами любых размеров. Можно также рассчитать, какой размер трещины допустим в материале, напряженном до заданного уровня. В реальных условиях ситуация несколько сложнее. Во-первых, выражение (1.4) для коэффициента интенсивности напряжений справедливо лишь для бесконечной пластины. Для пластины конечных размеров эта формула принимает вид (см. гл. III)
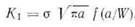
где W — ширина пластины. Для определения Kic необходимо знать функцию f(alW). Безусловно, f{alW) для малых значений alW стре^ мится к единице. Во-вторых, необходимо наложить ограничение на поперечные деформации в пластине. Истинное значение Kic можно получить опытным путем только в том случае, если перемещения точек пластины перпендикулярно ее плоскости достаточно малы, т. е. когда имеет место условие плоского деформирования, что наблюдается, Когда пластина имеет достаточную толщину (см. гл. IV, VII). Если
 § 1.4. Критерий Гриффитса
§ 1.4. Критерий Гриффитса
Несмотря на то что механика разрушения получила свое развитие главным образом за последние два десятилетия, одно из ее основных уравнений было получено Гриффитсом [9,10] еще в 1921 г. Рассмотрим бесконечную пластину единичной толщины с центральной поперечной трещиной длиной 2а. Края пластины неподвижны, а на-
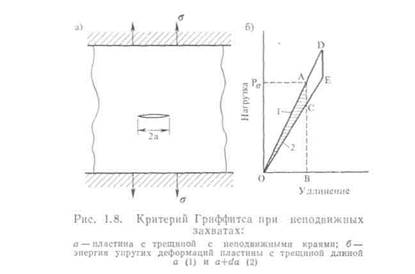
пряжение в ней равно σ, как показано на рис. 1.8, а. На рис. 1.8, ι приведена диаграмма «нагрузка — удлинение». Запасенная в пла стине упругая энергия представлена площадью ОАВ. Если длин трещины увеличится на величину da, то жесткость пластины умень шится (линия ОС); это означает, что нагрузка несколько уменьшит ся, поскольку края пластины неподвижны. Следовательно, упру гая энергия, запасенная в пластине, уменьшится до величины, рав ной площади ОСВ. Увеличение длины трещины с а до а + da приве дет к освобождению упругой энергии, равной по величине площад] О АС.
Если пластина нагружена до более высокого напряжения, то пр] увеличении длины трещины на величину da освободится больша; энергия. Гриффите предположил, что трещина будет расти лишь ι том случае, если освобождаемая при этом энергия достаточна дл! обеспечения всех затрат энергии, связанных с этим ростом. I противном случае необходимо увеличить напряжение. Треугольнш ODE представляет собой энергию, выделяемую при распространена трещины.
Условие, необходимое для роста трещины, следующее:
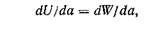
U —.упругая энергия, a W —-энергия, необходимая для роста рещины. Основываясь на расчетах поля напряжений для эллиптического отверстия, выполненных Инглисом [11], Гриффите получил выражение для dU/da в виде
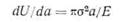
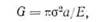
|
| на единицу толщины пластины, где Ε —модуль Юнга. Обычно величину dU/da заменяют величиной |
которая называется «скоростью высвобождения упругой энергии», приходящейся на каждую вершину трещины*. Величину G называют также трещинодвижущей силой; ее размерность —энергия, деленная на единицу толщины пластины и на единицу изменения длины трещины, что также может быть представлено в виде силы, приходящейся на единицу изменения длины трещины.
Энергию, расходуемую на распространение трещины, обозначают через R = dW/da и называют сопротивлением росту трещины. В первом приближении можно считать, что энергия, необходимая для образования трещины (для разрыва атомных связей), одинакова для любых приращений da. Это означает, что R —константа.
Теперь энергетическое условие (1.7) можно перефразировать следующим образом: для распространения трещин необходимо, чтобы G было, по крайней мере, равно R. Если R —константа, то, значит, величина G должна превысить некоторое критическое значение G4c. Следовательно, распространение происходит при следующем условии:
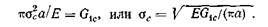
Критическое значение Gic (критическую скорость высвобождения энергии) можно получить, измерив напряжение ос, необходимое для разрушения пластины с трещиной размером 2а, и вычислив из уравнения (1.10) величину Gic.
Гриффите вывел свое уравнение для стекла — очень хрупкого материала. Он предположил, что величина R определяется только поверхностной энергией. В вязких материалах, например металлах, при вершине трещины образуются пластические деформации. Для образования новой зоны пластических деформаций при вершине трещины необходима большая энергия. Поскольку эта пластическая зона должна быть образована в процессе роста трещины, то энергию, необходимую для распространения трещины, можно положить равной энергии, необходимой для образования этой трещины. Это означает, что в металлах величина R определяется главным образом энергией Деформации в пластической зоне; поверхностная энергия в этом случае настолько мала, что ею можно пренебречь (см. [12, 13]). Энерге-
* Под «скоростью высвобождения упругой энергии» здесь следует понимать ее производную по длине трещины. (Прим. перев.)

 тический критерий есть необходимое условие распространения трещины. Этот критерий не обязательно должен быть достаточным. Если материал при вершине трещины не находится на грани разрушения, то трещина не будет расти даже при достаточной энергии для ее развития: материал должен до конца исчерпать свою способность воспринимать нагрузку и продолжать деформироваться. Однако последний критерий эквивалентен энергетическому критерию, поскольку из уравнений (1.2) и (1.9) следует, что
тический критерий есть необходимое условие распространения трещины. Этот критерий не обязательно должен быть достаточным. Если материал при вершине трещины не находится на грани разрушения, то трещина не будет расти даже при достаточной энергии для ее развития: материал должен до конца исчерпать свою способность воспринимать нагрузку и продолжать деформироваться. Однако последний критерий эквивалентен энергетическому критерию, поскольку из уравнений (1.2) и (1.9) следует, что
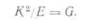
Очевидно, критерий по напряжениям и энергетический критерий вы-1 полняются одновременно. Следовательно, уравнения (1.4) и (1.10)1 эквивалентны. В гл. III будет показано, что уравнение (1.11) спра.-| ведливо для случая плоского напряженного состояния, а в случае! плоского деформированного состояния его следует дополнить коэф-I фициентом (1 —м2), что приведет к соотношениям
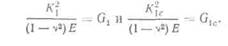
Дата добавления: 2015-06-22; просмотров: 4960;
