Форма зоны пластичности

До сих пор рассматривался вопрос о протяженности зоны пластичности только вдоль оси χ — в ^-направлении, и для простоты временно было сделано предположение о том, что зона пластичности имеет форму круга. Более точное представление о форме этой зоны можно получить, рассматривая условие текучести для углов Θ, отличных от нуля (см. [9, 10]). При этом обычно применяют условие текучести Треска или Мизеса. По условию Треска, текучесть наступает, когда максимальное касательное напряжение т_Шах превышает предел текучести при сдвиге o_yJ2. Условие текучести Мизеса в главных напряжениях задано соотношением

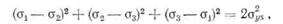
где o_ys —предел текучести в одноосных испытаниях. При испытании на растяжение 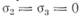, откуда следует, что текучесть наступает При Oi s=a O_ys.

Уравнения, описывающие поле напряжений при вершине трещины в главных осях, были получены в (3.55) гл. III:

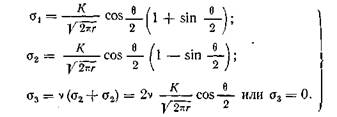
На плоскости θ — 0 главные напряжения равны между собой и действуют в направлении осей χ и у; напряжение а_у является главным. Для плоского напряженного состояния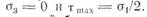

Следовательно, тот размер зоны пластичности, который оыл получен в § 4.1, действительно определяет зону пластичности как по условию текучести Треска, так и по условию текучести Мизеса.

Границу зоны пластичности как функцию θ можно найти, подставляя уравнения (4.18) в соотношения (4.17). Таким образом получим:

Зависимость расстояния от вершины трещины до границы зоны пластичности можно представить в следующем виде:

для плоской деформации \

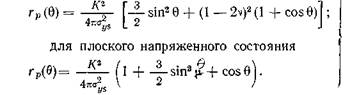
Если предположить в уравнении для плоского напряженного состояния θ ;= 0, то действительно получится соотношение (4.1).

Граница зоны пластичности в том виде, как она задана уравнениями (4.20), изображена в безразмерном виде на рис. 4.5. Зона

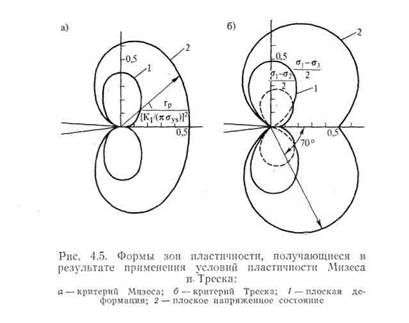
пластичности для плоской деформации заметно меньше зоны пластичности в случае плоского напряженного состояния: из уравнений (4.20) следует, что при 9 = 0 и ν = 1/3 их размеры отличаются друг от друга в девять раз. Поэтому корректировочный коэффициент на зону пластичности, заданный соотношением (4.1), в случае плоской деформации неприменим (см. § 4.5).

Если используется условие текучести Треска, то форма зоны пластичности получается несколько иной. С помощью кругов Мора находим, что максимальное касательное напряжение в случае плоского напряженного состояния τ _max — ο"ι/2, а в случае плоской деформации 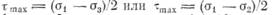в зависимости от того, что больше. С помощью уравнений (4.18) получаем зону пластичности Треска в следующем виде:

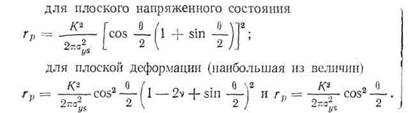
Уравнения (4.21) позволяют определить форму зоны пластичности Треска, как показано на рис. 4.5, б. Зоны Треска имеют несколько большие размеры и другую форму по сравнению с зонами Мизеса.