Распространение трещины

Как было показайо в § 1.3, коэффициент интенсивности напряжений есть мера напряжений и деформаций в окрестности вершины трещины. Коэффициент интенсивности напряжений сохраняет свое значение лишь тогда, когда пластическая зона мала. В этом случае можно также ожидать, что степень распространения трещины за цикл определяется коэффициентом интенсивности напряжений. Если две различные трещины имеют два одинаковых распределения напряжений, т. е. равные коэффициенты интенсивности напряжений, то они должны распространяться с одной и той же скоростью.

Если циклическая нагрузка меняется от нуля до некоторой положительной величины (постоянной амплитуды), то коэффициент интенсивности напряжений меняется в интервале

где /Cmm :=⁵ 0. Следовательно, распространение трещины за один цикл при циклическом процессе нагружения (скорость распространения трещины) есть величина, зависящая от амплитуды изменения интенсивности напряжений ΔΚ-

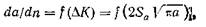
где S_a —амплитуда изменения напряжения (символ S —общепринятое в литературе обозначение циклических напряжений). Пэрис, Гомез и Андерсон [16] первыми пришли к этому выводу и проверили его на практике. Если использовать результаты только одного испытания, то уравнение (1.13), очевидно, удовлетворится автоматически: в этом случае любая зависимость da/dn от Δ/С подтвердит уравнение

Рассмотрим результаты двух испытаний на распространение трещин, изображенных на рис. 1.9, а. Амплитуды изменения напряжений были одинаковыми и постоянными в каждом испытании. Скорость распространения трещины, очевидно, увеличивалась с ростом трещины. Скорость dddn можно определить из наклона кривых. Величина Δ К получается из соотношения 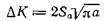при подстановке соответствующего значения а. На рис. 1.9, б график зависимости da/dn от Δ/C изображен в логарифмическом масштабе по обеим осям. Данные, полученные при больших амплитудах изменений напряжений, указывают на сравнительно большие значения ΔΚ и

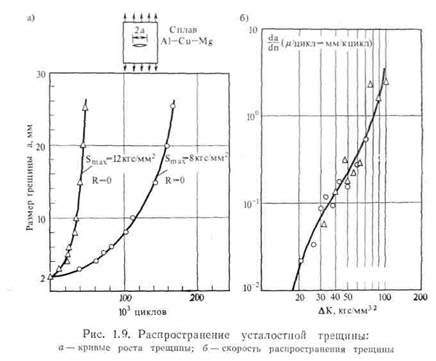
daldn в начале процесса. Другие данные получены при малых величинах АК и daldn, которые, однако, достигают таких же больших значений, как и в первом испытании.

Данные двух испытаний, выполненных при различных условиях, располагаются на одной кривой, что подтверждает полезность уравнения (1.13). Очевидно, между двумя испытаниями, из которых в одном имеется маленькая трещина и большое напряжение, а в другом — длинная трещина и малое напряжение, нет никакой разницы, если величины АК в них одинаковы; в обоих испытаниях скорость распространения трещины одна и та же.

На графике зависимости daldn от АК, построенном в логарифмическом масштабе по обеим осям, экспериментальные точки часто ложатся на прямую линию. Поэтому уравнение (1.13) было принято в виде

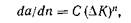
где Сип — константы. Было получено большое количество значений п, которые обычно лежали в пределах от 2 до 4. Однако уравнение (1.14), как оказалось, плохо согласуется с данными испытаний. На практике график зависимости daldn от АК имеет форму буквы S или, по крайней мере, состоит из участков разного наклона (см. [17, 18]). В испытаниях, связанных с ограниченным диапазоном изменения АК, получена экспоненциальная зависимость типа (1.14); в этом случае значение η зависит от величины амплитуды АК (большие, малые и

_промежуточные значения ΔΚ). Когда трещина достигает критического размера, при котором отношение daldn обращается в беско-_нечность, при определении максимального значения амплитуды ΔΚ могут появиться погрешности. Общее разрушение происходит за один цикл, в котором интенсивность напряжений достигает К и-

Циклическое напряжение определяется двумя параметрами: амплитудой S_a и средним напряжением S_m. Если S_m = S_a, то минимальное напряжение за цикл равно нулю. Это означает, что максимальная интенсивность напряжений за цикл К_тах = ΔΚ. Если S_m > S_a, το максимальная интенсивность напряжений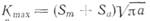

превышает значение ΔΚ- Не вызывает сомнений, что скорость роста трещины зависит от максимальной интенсивности напряжений. Поэтому более общей формой уравнений (1.13) является соотношение

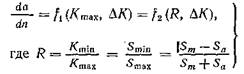
и называется коэффициентом асимметрии цикла (см. гл. X).

Докритический медленный рост раковины может происходить не только под действием циклических нагрузок, но и за счет других механизмов, из которых наиболее важным является механизм коррозионного растрескивания под напряжением. Как и в случае роста усталостной трещины, скорость роста коррозионной трещины при заданных условиях взаимодействия материала со средой (а следовательно, и время до разрушения) определяется коэффициентом интенсивности напряжений. Одинаковые образцы с одинаковыми начальными трещинами, но нагруженные до различных напряжений (разные начальные значения К,), разрушаются через различное время (см. [19]), как показано схематически на рис. 1.10. Образец, нагружен-

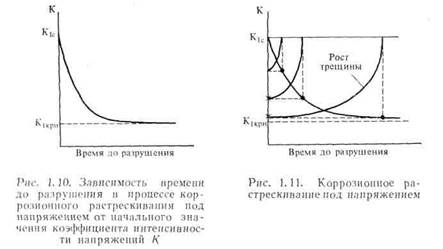
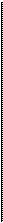ный до значения К\с, разрушается сразу. Образцы, нагруженные] до значений К, меньших определенного порогового уровня, не разЛ рушаются никогда; это пороговое значение обозначают через Ллк_Рн,1 где индекс «крн» означает коррозионное растрескивание под напря* жением.

В процессе коррозионного растрескивания под напряжением нагрузка может оставаться постоянной. Поскольку трещина расши-1 ряется, интенсивность напряжений непрерывно увеличивается. В ре-1 зультате скорость роста трещины за единицу времени daldt увеличи-1 вается в соответствии с уравнением

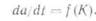
Когда трещина достигает размера, при котором К становится равным К\с, происходит окончательное разрушение, как показано на рис. 1.11.

Пороговое значение коэффициента Кы_Рн для процесса корро--зионного растрескивания под напряжением и скорость роста трещи-

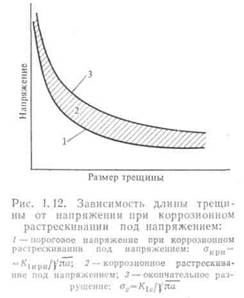
ны зависят от материала и условий окружающей среды. Из рис. 1.12 следует, что деталь с трещиной определенного раз-' мера, нагруженная до такого напряжения σ, что а]/па ^= К\с, разрушается в самом начале процесса нагружения. В деталях, нагруженных до значений /<", равных или больших /<Ίκ_Ρη (заштрихованная область), трещина будет расти вплоть до разрушения. Положения механики разрушения применимы к коррозионному растрескиванию под напряжением, однако ее возможности в этом плане пока еще весьма ограничены. Поэтому в настоящей книге задачам коррозионного растрескивания под напряжением уделяется небольшое внимание.

Заключение

Было показано, что процессы распространения трещины и разрушения определяются коэффициентом интенсивности напряжений. Этот коэффициент играет в механике разрушения определяющую роль. В принципе, зная коэффициент интенсивности напряжений для трещины в данном элементе конструкции, можно рассчитать процесс роста трещины и время до разрушения. Иными словами,на все вопросы, поставленные в § 1.2, могут быть даны ответы. К сожалению, напрактике встречается так много осложнений, что применить, кажется, простые положения, рассмотренные в данной главе, не всегда представляется возможным. Однако во многих случаях можно получить полезные результаты. Для правильной оценки области применения механики разрушения в технике проектировщик и инженер должны обладать достаточными сведениями о физических принципах и допущениях, лежащих в ее основе. Наука «Механика разрушения» еще далека от завершения и не является простым инструментом проектирования. В последующих главах будут выявлены достоинства и недостатки этих положений.