Глава VI. ДИНАМИКА РОСТА ТРЕЩИНЫ И ЕГО ТОРМОЖЕНИЕ§ 6.1. Скорость распространения трещины и кинетическая энергия

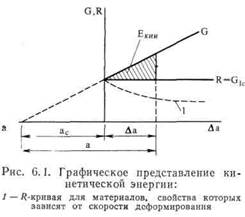
До сих пор рассматривалась задача о медленном росте трещины и о нестабильности этого процесса перед началом разрушения. В данной главе рассматривается вопрос о поведении трещины после возникновения нестабильности. Нестабильность, предшествующая разрушению, возникает тогда, когда при расширении трещины интенсивность выделения энергии упругих деформаций G постоянно превышает сопротивление росту трещины R. Избыток выделенной энергии (G — R) может перейти в кинетическую энергию. Эта кинетическая энергия связана с быстрым движением точек среды по обе стороны от траектории трещины при ее прохождении с большой скоростью. Разница между G и R определяет количество энергии, которое может перейти в кинетическую; следовательно, эта величина определяет скорость, с которой эта трещина будет распространяться в среде. Величины G и R представляют собой энергию, связанную с распространением трещины на Δα. Следовательно, общее количество энергии, которое может перейти в кинетическую энергию, после того как размер трещины увеличится на Δα, определяется интегралом от (G — R) на отрезке Δω. Этот интеграл представлен на рис. 6.1 заштрихованной областью.

Изображенный на рис. 6.1 случай основан на трех упрощающих предположениях:

1) процесс распространения трещины происходит при постоянном напряжении;

2) интенсивность выделения энергии упругих деформаций не зависит от скорости распространения трещины;

3) сопротивление росту трещины постоянно.

Что касается третьего предположения, то в предыдущей главе было показано, что во многих случаях величина R есть возрастающая функция, по крайней мере вовремя медленного распространения трещины. Этот факт не вносит существенных изменений в основные положения данной главы. Однако на величину R оказывает влияние

другое обстоятельство, которым нельзя пренебречь. Сопротивление росту трещины зависит от поведения материала при пластическом деформировании вблизи вершины трещины и его прочностных характеристик. Известно, что эти характеристики зависят от скорости деформирования. Поведение многих материалов зависит от скорости деформирования: при более высоких скоростях деформирования предел текучести увеличивается, а деформация, при которой происходит разрушение, уменьшается. При вершине распространяющейся с большой скоростью трещины скорости деформирования очень велики, поэтому следует ожидать, что при больших скоростях распространения трещины материал будет проявлять больше хрупких свойств. В результате материалы, свойства которых зависят от скорости деформирования, имеют убывающую 7?-кривую, показанную на рис. 6.1 штриховой линией.

Второе предположение означает, что решение упругой задачи о статическом поле напряжений применимо и в динамическом случае. В действительности распределения напряжений в этих двух случаях из-за введения членов, зависящих от времени, различны. Этой задаче посвящен § 6.2. А в настоящем параграфе предполагается, что решение статической задачи приблизительно верно и для динамического случая.

Первое предположение о неизменности напряжения несущественно. Ясно, что нестабильный рост трещины происходит при постоянной внешней нагрузке. Так как это является ограничивающим фактором, последующие рассуждения приводят к оценке верхней границы скорости распространения трещины. На практике во время роста трещины величина нагрузки может уменьшаться, что приводит к уменьшению G и, следовательно, к уменьшению значения (G — R) при условии, что величина R постоянна.

Основываясь на теории размерностей, Мотт [1] получил выражение для кинетической энергии трещины. Элемент пластины с трещной, находящийся за вершиной этой трещины, перемещается на расстояния и и υ (см. гл. III), заданные соотношениями

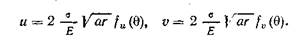(6.1)

Если вершина трещины передвигается, то выделенный элемент будет от нее удаляться: расстояние г от этого элемента до вершины трещины пропорционально размеру трещины. Следовательно, и перемещения пропорциональны размеру трещины:

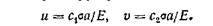(6.2)

Если с течением времени трещина растет, то эти перемещения также увеличиваются. Скорости этого движения соответственно равны:

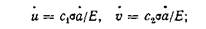(6.3)

в соотношении (6.3) точка означает производную по времени. Элемент среды массы т, движущийся со скоростью V, имеет кинетическую энергию mV²/2. Следовательно, кинетическая энергия материала пластины с трещиной, который движется со скоростями и и υ,

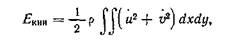(6.4)

где ρ — удельная плотность. Следует заметить, что уравнение (6.4) справедливо для пластины единичной толщины. Подставляя в уравнение (6.4) соотношения (6.3), получим

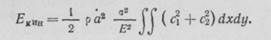(6.5)

В случае бесконечной пластины размер трещины α является единственным характерным размером, имеющим размерность длины. Площадь, вдоль которой выполняется интегрирование, должна быть пропорциональна а². Это означает, что результат интегрирования должен быть пропорционален fea², где k — константа:

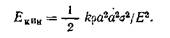(6.6)

Кинетическая энергия пропорциональна квадратам размера трещины и напряжения. Совершенно очевидно, что она должна быть пропорциональна удельной массе и квадрату скорости распространения трещины.

Используя рис. 6.1, можно получить другое выражение для кинетической энергии:

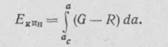(6.7)

Рассматривая случай, когда R — константа, а величина G при по-

стоянном напряжении определяется решением статической задачи, получаем выражение для кинетической энергии

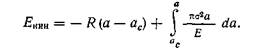
Константа R в начале нестабильного процесса равна G\_c (величина которого задана соотношением G\_c =no²ajE). Подставляя в соотношение (6.8) равенство R = G\_c и проводя интегрирование, получаем (для двух вершин трещины)

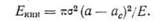
Два выражения (6.6) и (6.9) для кинетической энергии можно приравнять друг к другу, получив

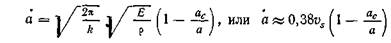
Выражение 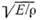есть скорость продольных волн в среде, т. е. оно

равно скорости звука v.. Значение 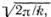как оказывается, равно

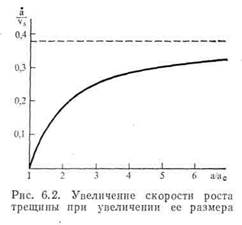
приблизительно u,do. Уравнение (6.10) описывает рост скорости распространения трещины от нуля при а =а_с до верхней границы скорости 0,38u_s, когда a J а стремится к нулю; это имеет место тогда, когда трещина вырастает достаточно для того, чтобы выполнялось соотношение а » а _с. На рис. 6.2 представлено графическое изображение соотношения (6.10). В работе Берри [3] выполнены подобные вычисления для образцов, имеющих форму двухконсольной балки. То же самое было сделано Хоаглэндом [41. Интегри-

рование соотношения (6.7) можно провести и в том случае, если величина R является возрастающей функцией при условии, что эта зависимость R от размера трещины известна. Если для аппроксимации ^-кривой принята простая степенная функция (см. гл. VIII), то, как оказывается (см. [5]), результат вычислений все равно приводит к ограничению скорости распространения трещины величиной v_s~\/2n/k.

Измеренные скорости распространения трещин лежат значительно ниже их теоретических значений, вычисленных с помощью уравнения (6.10). В работе Блама [2] собраны результаты этих измерений. Некоторые из этих данных для трещин в хрупких материалах, полу-

, пока не существует.