Емкости высокого давления и трубопроводы
К стальным конструкциям вообще и к емкостям высокого давления в частности применяют критерии разрушения, отличные от концепций механики разрушения, изложенных в настоящей работе; это испытание Шарпи, испытание падающим грузом (см. [3]), испытания на торможение трещины (см. [4]) и диаграмма анализа разрушения (см. [5]). Здесь не место рассматривать полезность всех этих подходов. Подробное обсуждение их использования и применимости можно найти в многочисленной литературе (например, [5—9]). Далее будут рассмотрены только те методы механики разрушения, которые позволяют провести количественный расчет прочности конструкции, причем рассмотрено только их применение к чрезвычайно вязким материалам.
В тонкостенной емкости высокого давления или трубопроводе может^ развиться продольная трещина. Напряжение, действующее поперек трещины, есть окружное напряжение σΗ = pRlB, где R — радиус емкости или трубы, В — толщина стенки, а ρ — внутреннее давление. Для сквозной трещины, имеющей длину 2а, коэффициент интенсивности напряжений задан соотношением
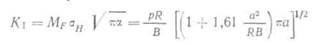
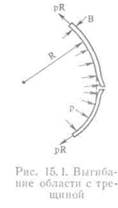
В (15.1) Мр — коэффициент увеличения интенсивности напряжении, который был теоретически получен Фолиасом [10]. Необходимость в этом коэффициенте определяется тем, что края трещины под действием внутреннего давления выгибаются наружу, как показано на рис. 15.1. По Фолиасу, коэффициент -увеличения

Для коэффициента MF было предложено
несколько других (эмпирических) выражений (см. [11—14]). Лучше всего использовать результат Фолиаса, по крайней мере потому, что его подтверждают результаты прекрасной программы испытаний труб
|
при различных давлениях, выполненных Даффи, Айбером, Мэкси, Мак Клуром и Кифнером [15—■ 20]. Этими исследователями были испытаны различные трубы, имеющие значительную длину. Поскольку применявшиеся в этих испытаниях образцы были выполнены из низкопрочных материалов (из сталей с пределом текучести, меняющимся в пределах от 25 до 120 кси), была использована коррекция выражения для К на зону пластичности в виде уравнения (15.1). В более ранней работе [20] этими авторами была использована коррекция на зону пластичности Дагдейла [21] (см. гл. IV):
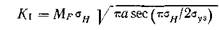
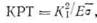
|
| и принимая для определения КРТ решение Дагдейла |
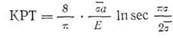
|
Для того чтобы учесть влияние работы упрочнения, величина 2вуа в (15.2) была заменена на oys + au. В более поздней работе этими авторами была использована коррекция на зону пластичности Хана и др. [22], рассмотренная в гл. IjX. Заметив, что
можно получить выражение для коэффициента интенсивности напряжений. В этих уравнениях σ — эффективный предел текучести, учитывающий работу упрочнения. Заменяя σ на Мр<Ун и объединяя уравнения (15.3) и (15.4), получаем
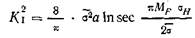
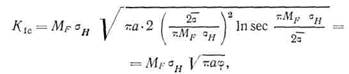
|
| где φ — поправка на пластичность. Из этого уравнения следует, что |
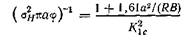
|
Можно ожидать, что разрушение произойдет при Κι = Κι с Для данного материала. Величину σ можно определить эмпирически. Оказывается, для большинства используемых для изготовления труб сталей σ « oys + 10 кси. В работе Хана и других уравнение (15.5) записано в виде
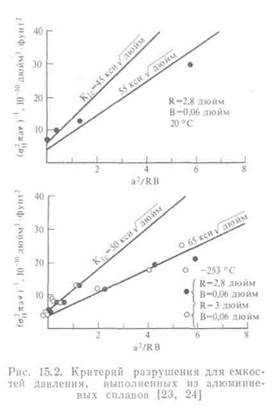
Справедливость этого критерия можно проверить, подставляя в (15.7)
разрушающие значения он и строя график зависимости (σ^παφ)-1 от a?/(RB). Этот график должен представлять собой прямую линию.. Хан и другие построили эти графики для большого количества данных испытаний емкостей давления, взятых ими из различных источников (рис. 15.2). Значения К\с, полученные в испытаниях емкостей давления, находятся в определенном согласии с соответствующими значениями, полученными при испытании плоских пластин, изготовленных из тех же материалов (см. [22]). Разброс этих данных можно частично отнести за счет запечатывания длинных трещин, которое предпринималось для избежания падения давления в емкости (см. [22]).
Если разрушающее напряжение очень близко к пределу текучести (т. е. в случае очень коротких трещин или в случае большой вязкости),
то критерий разрушения определяется главным образом величиной коэффициента коррекции^на пластичность^На рис. 15.3 представлено графически соотношение между ΜΡσΗ/σ~ и πK2ic/(8aa2), полученное с помощью уравнения (15.5)^ Оказывается, для больших значений π Kic/(8aa3) значение MF aH/a приближается к единице. В этих
|
случаях разрушающее напряжение не зависит от вязкости разрушения, т. е. критерий разрушения принимает вид
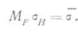
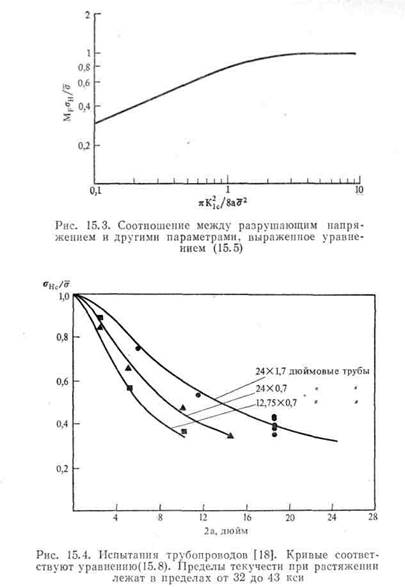
Согласно уравнению (15.8), разрушение наступает тогда, когда возникает общая текучесть, или немного позже. Это условие разрушения было рассмотрено в гл. IX. На рис. 15.4 представлены данные, полученные Айбером и др. [18] для трубопроводов. Эти данные подтверждают применимость уравнения (15.8) к материалам с высокой вязкостью.
Разрушения труб и тонкостенных емкостей давления могут происходить посредством скола, однако микромеханизм отделения в зависимости от температуры может быть также вязким. В последнем случае с инженерной
точки зрения разрушения все-таки носят хрупкий характер: они связаны с малыми пластическими деформациями и происходят с большими скоростями. Результаты измерения скоростей распространения трещин при сколе (см. [15]) показали, что их значения лежат в пределах от 1500 до 2500 фут/с. В случае, когда микромеханизм отделения был вязким, измеренные значения скоростей имели порядок 600 фут/с.
Трещины в трубопроводах могут распространяться на несколько миль, что приводит к большим разрушениям, если не возникают условия остановки этих трещин. Задержка трещины зависит от природы и сжимаемости транспортируемого по трубопроводу вещества. В случае, когда этим веществом является вода или нефть, происходит падение давления за счет утечки; окружное напряжение при этом умень-
шается. В результате может уменьшиться величина К, однако это произойдет лишь в том случае, если уменьшение К за счет понижения давления будет происходить быстрее, чем его увеличение за счет увеличения размера трещины. В случае, когда транспортируемая среда является газом, степень понижения давления зависит от скорости распространения трещины и скорости звука в этом газе (волны декомпрессии).
На рис. 15.5 представлена теоретическая кривая (см. [15, 16, 25]), по которой можно определить значения отношения напряжения при вершине трещины к его начальному уровню для различных скоростей роста трещины. Кривая, изображенная на этом рисунке, применима только к трещинам, которые уже распространились на некоторое расстояние, иначе прорезь была бы слишком мала для значительного по-
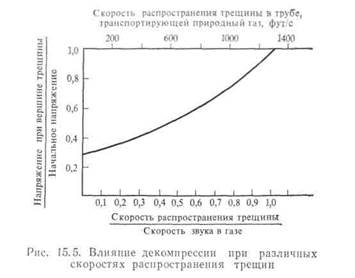
нижения давления. Если бы, после того как трещина распространилась на некоторое расстояние, скорость ее распространения уменьшилась до нуля, то давление в трубе составляло бы почти 30% от исходного уровня. В случае, когда скорость роста трещины равняется скорости звука в газе, уменьшение давления при вершине трещины несущественно. Скорость звука в природном газе равна 1300 фут/с (верхняя масштабная линия на рис. 15.5); это означает, что трещина, образующаяся за счет хрупкого разрушения и бегущая со скоростью 2000 фут/с, из-за недостаточного понижения давления не останавливается. Вязкие трещины, бегущие со скоростью' 600 фут/с, вероятно, можно остановить.
Полагая, что кинетическая энергия в процессе разрушения не играет никакой роли, считаем, что критерий остановки трещины можно получить, подставляя в уравнение (15.5) значение Κι = KarreSf Даже в случае, если известно значение Karrest, применение этого критерия было бы затруднительно, поскольку неизвестно, как определить скорость роста трещины. Эту скорость нужно знать для того, чтобы рассчитать напряжение при вершине трещины (рис. 15.5) и чтобы знать мгновенный размер трещины, значение которого можно было бы подставить в уравнение (15.3). Максей и др. [15, 16] обошли эту проблему, предполагая, что: 1) интенсивность высвобождения
энергии, необходимая для остановки трещины, равна своему начальному значению; 2) значение этой критической скорости высвобождения энергии для вязких трещин можно получить из верхнего плато Шарли. Таким образом, можно предсказать возможность торможения вязкой трещины. Максей и другие представили данные, полученные ими с помощью уравнения (15.8), в виде графика, подобного показанному на рис. 15.3. Полученные ими данные представлены
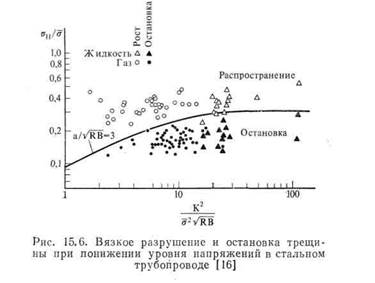
на рис. 15.6, на котором σΗ — окружное напряжение на соответствующем этапе декомпрессии. Кривая, изображенная на рис. 15.6, получена при отношении a/]/ RB = 3 и соответствующем значении MF = 3,3. Совершенно очевидно, что эта линия определяет уровень, на котором происходит остановка трещины, и что 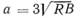 есть максимальный эффективный размер трещины; процесс распространения более длинных трещин происходит так, будто их длина равна
есть максимальный эффективный размер трещины; процесс распространения более длинных трещин происходит так, будто их длина равна
Трещина в емкости давления обычно образуется как поверхностная трещина на внутренней части стенки. Можно ожидать, что в тонкостенных емкостях эта раковина будет расти при напряжениях, меньших критических (за счет усталостных процессов или при коррозии под напряжением), пока она не перерастет в сквозную трещину. После этого появляется возможность обнаружить эту трещину, прежде чем ее размер станет критическим, поскольку в емкости появляется утечка. При более жестких условиях только что образовавшаяся сквозная раковина может уже стать критической. Эта раковина скачком проникнет через стенку и, если условия на стенке критические, будет продолжать распространяться как сквозная трещина. В противном случае может произойти мгновенная остановка, за которой
последует утечка (обнаруживаемая). На практике чрезвычайно важно, чтобы процесс разрушения протекал именно так. В последующих параграфах рассматривается так называемый критерий утечки до разрушения.
Возникновение утечки до разрушения в толстостенных емкостях маловероятно. Используемые в реакторах емкости с толщинами стенок порядка 0,15 м встречаются не так уж редко. Критическая раковина может быть либо эллиптической поверхностной трещиной, либо угловой трещиной. Трудности, встречающиеся при расчете характеристик роста и разрушения таких раковин, рассмотрены в нескольких параграфах настоящей работы. В принципе поверхностные раковины в емкостях давления можно рассматривать так же, как в любой другой конструкции. На практике же оказывают влияние несколько осложняющих факторов. Внутреннее давление в емкости действует на внутренние стенки трещины. Интенсивность напряжений, возникающую под действием этого давления, следует добавить к интенсивности, возникающей под действием нормального напряжения. В гл. III было отмечено, что это можно сделать, просто добавив внутреннее напряжение к действующему:
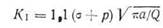
|
Второй проблемой, связанной с толстостенными емкостями, является изменение напряжения в сечении стенки. Наибольшую величину имеет напряжение во внутренней части стенки. Поэтому интенсивность напряжений на конце главной оси эллипса
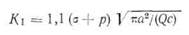
может быть наибольшей, что зависит от отношения напряжений, заданных уравнениями (15.9) и (15.10), а также от отношения ale (предполагается, что главная ось раковины направлена в продольном направлении, а малая — в направлении толщины). Это усложняет исследование поведения поверхностной раковины при разрушении, которое было рассмотрено в гл. XI.
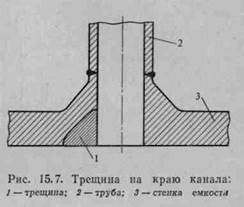
Трещины и раковины обычно возникают в зонах концентрации напряжений, например на краю отверстия. В емкости давления местом, предрасположенным к растрескиванию, является канал, соединяющий трубу с емкостью. Обычно эта область для уменьшения концентрации напряжений усилена, и сварные швы расположены вне наиболее опасной области. Эта зона может быть спроектирована так, как показано на рис. 15.7. При анализе процесса распространения трещины на краю канала встречаются следующие трудности:
а) по сечению трещины имеется большой перепад напряжений;
б) трещина находится в области концентрации напряжений;
в) по причинам, указанным в пп. а и б, коэффициент интенсив
ности напряжения существенно меняется вдоль фронта трещины.
Маловероятно, чтобы трещина в этих условиях приняла форму эл
липса или круга;
г) сложная система напряжений и неопределенная форма рако-
вины порождают множество проблем, возникающих при определении К',
д) знание величины К и ее изменения вдоль принятого фронта трещины еще не дает возможность определить изменение этого фронта во время докритического роста трещины (усталостного или коррозионного под напряжением). Необходимо знать параметры рас-
|
пространения трещины в различных направлениях.
Для решения такой задачи имеется несколько возможностей. Для дорогостоящих реакторных емкостей оправдано проведение широкой программы исследований. Поэтому представляется разумным начать с некоторого частного испытания, в котором имитируется одно вполне определенное место, например испытание плоской пластины на одноосное или двухосное растяжение. Образец может иметь начальную ракови-
ну, которая в процессе циклического нагружения будет расти. Несколько однотипных испытаний можно прекратить на различных этапах распространения трещины, после чего подвергнуть пластину действию разрушающей нагрузки. Полученные при этом поверхности разрушения дадут возможность определить, как изменяется форма трещины.
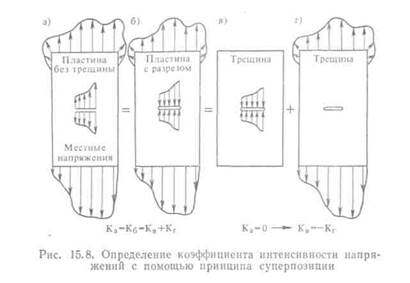
Экспериментально определенные формы раковин можно использовать для определения коэффициентов интенсивности напряжений. В этом случае можно применять анализ методом конечных элементов (см. гл. XIII). Ввиду градиентов напряжений, действующих поперек трещины, лучше всего определить интенсивность напряжений с помощью следующей методики. Во-первых, поле напряжений в области с трещиной определено только в том месте, где трещины нет. Когда трещина прорезает данную область, эти напряжения существовать более не могут. Определить коэффициент интенсивности напряжений в этом случае можно, рассматривая трещину с внутренними расклинивающими силами, распределение которых равно распределению внутренних разрывных напряжений в данном месте, и используя принцип суперпозиции (рис. 15.8, а—г).
После того как величина К определена, результаты испытаний можно подвергнуть дальнейшему анализу. Процесс распространения трещины можно привести в соответствие с вычисленным значением К, а также с данными, полученными при испытании простых образцов. Кроме того, можно определить значения К, при которых происходит разрушение, и сравнить результат с имеющимися данными о значениях К\с- Это до некоторой степени подтвердило бы вычисленные значения К- Последнее может быть применимо к реальным емкостям
при условии использования коррекции для учета внутреннего давления так, как это было сделано в уравнениях (15.9) и (15.10). Вряд ли необходимо говорить о том, что эта методика может быть применена не только для анализа емкостей давления; с таким же успехом ее можно использовать и для анализа других сложных конструкций.
§ 15.3. Критерий «утечки до разрушения»
Трещина, образовавшаяся на внутренней части оболочки тонкостенной емкости давления за счет циклических процессов или коррозии под напряжением, может расти и, наконец, достичь внешней стороны стенки. После этого образуется утечка емкости, что дает реальную возможность обнаружить эту трещину. Однако существует и вероятность того, что нестабильность, предшествующая разрушению, возникнет уже при наличии поверхностной раковины. Если при этом разрушение останавливается после того, как трещина проскакивает сквозь стенку, в емкости образуется утечка и есть время для того, чтобы обнаружить трещину прежде, чем эта «сквозная» трещина вновь достигнет критического размера. Емкость, разрушение которой происходит подобным образом, удовлетворяет критерию утечки до разрушения.
Ирвином и несколькими другими авторами [26—28] был предложен упрощенный критерий утечки до разрушения. Он основан на предположении о том, что перед проскакиванием трещины через стенку соответствующая ей поверхностная раковина имеет форму полукруга; это означает, что сквозная трещина в момент проскакивания имеет длину, равную удвоенной толщине стенки (рис. 15.9). Предполагается, что нестабильность, предшествующая разрушению в трещине размера 2В, возникает при напряжении, равном пределу
текучести ays. Предполагается также, что при столь высоком напряжении имеет место плоское напряженное состояние. Следовательно, остановка может произойти, если ударная вязкость при плоском напряженном состоянии Kic не меньше, чеыа Уп(В-\-Гр ):
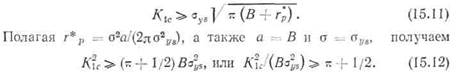
|
Окончательное уравнение (15.12) до некоторой степени отличается от того, что предполагалось вначале (см. [26—28]). Причиной расхождения может быть тот факт.
|
что при выводе коррекции на пластичность предполагалось, что зона пластичности мала по сравнению с размером трещины, а при выводе уравнения (15.12) этого предположения сделано не было. Критерий, выраженный уравнением (15.12), слишком упрощен и находит лишь ограниченное применение в качестве критерия утечки до разрушения, потому что его применимость ограничена случаем разрушения в условиях общей текучести. Кроме того, это уравнение непригодно для поверхностных раковин, длина которых превышает две толщины; оно
также не предсказывает реальные условия остановки. Даффи и др. [20] предложили эмпирический критерий утечки до разрушения, основанный на данных испытаний и пригодный для труб всех размеров.
Более общий критерий утечки до разрушения можно получить, используя принципы, принятые в механике разрушения. Условие разрушения для поверхностной раковины следующее:
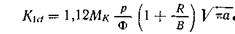
В уравнении (15.13): Кш — вязкость разрушения для материала с трещиной, распространяющейся в направлении толщины; Μ/ς — коэффициент увеличения интенсивности напряжений Кобаяши [29], учитывающий приближение фронта трещины к свободной поверхности (см. гл. III). Окружное напряжение ан в тонкостенной емкости равно pRlB. Добавляя к напряжению величину р, мы учитываем
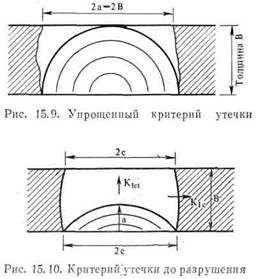
внутреннее давление, действующее внутри трещины. Малая ось раковины, как показано на рис. 15.10, равна а. Разлагая функцию φ в ряд, как было сделано в гл. III, получаем для давления pi, необходимого для возникновения процесса нестабильного роста поверхностной раковины, следующее выражение:
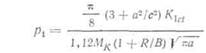
|
Поверхностная раковина перерастет в сквозную трещину с размером 2с. Согласно уравнению (15.1), давление р2, вызывающее нестабильное распространение сквозной трещины, задано соотношением
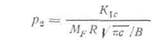
|
где Мр — коррекция Фолиаса, учитывающая выгибание краев трещины, а К\с — вязкость разрушения для материала с трещиной, распространяющейся в продольном направлении.
Остановка трещины может произойти только в том случае, если давление, необходимое для распространения сквозной трещины, имеющей длину 2с, больше, чем напряжение, необходимое для нестабильного роста раковины, имеющей глубину а. Следовательно, критерий утечки до разрушения следует из неравенства р2 > р\, которое с помощью уравнений (15.14) и (15.15) можно преобразовать к виду
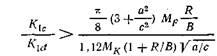
Для тонкостенных емкостей с большим отношением RIB единицей по сравнению с RIB можно пренебречь. Поверхностные раковины обычно имеют размер порядка нескольких толщин пластины; получающаяся в результате сквозная трещина имеет тот же размер, и поскольку отношение RIB велико, коррекция Фолиаса на величину р2 не влияет (Mf « 1). В этом случае уравнение (15.16) можно преобразовать к виду
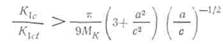
Прежде всего рассмотрим раковины, для которых отношение а!В еще мало или М% « 1 (см. гл. III). В этом случае правую часть соотношения (15.17) вычислить несложно; графическое изображение этого неравенства представлено на рис. 15.11. Включение коррекции Кобаяши сопряжено с некоторыми трудностями, поскольку М% зависит от отношения а/В. Для пологих раковин, если а/В « 1, М% имеет порядок 2. Поэтому нижняя линия на рис. 15.11 начинается при значении KiJKict, составляющем примерно 50% от соответст-
вующего значения для верхней линии. Для полукруглых раковин Μ χ близко к единице независимо от а/В. Таким образом, в правой части диаграммы обе линии совпадают, что дает возможность найти нижнюю границу критерия для а/В « 1.
Совершенно очевидно, что условие утечки до разрушения более легко выполняется в материалах, обладающих значительной анизотропией. На практике анизотропия в отношении вязкости разрушения
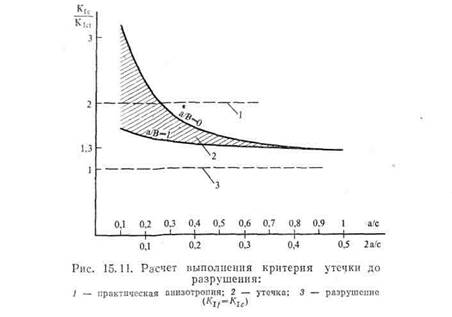
редко больше, чем 2 (см. гл. II). Это означает, что добиться выполнения условия утечки до разрушения для трещин, глубина которых меньше величины, определяемой соотношением а/с « 0,3, сложно.
Чтобы использовать уравнение (15.11), необходимо преодолеть одно небольшое затруднение, заключающееся в том, что, как было отмечено в гл. XI, критическая интенсивность напряжений Кц, при которой раковины становятся нестабильными, лежит где-то в пределах между К\с и Км- На рис. 15.11 отношение Kiel Км следовало бы заменить на KiJKif- Для пологих раковин Кц близко к К\с\ это означает, что левая часть рис. 15.11 остается справедливой. Следует ожидать, что полукруглые раковины начнут распространяться при Кц, близком к Ки', это означает, что условие утечки до разрушения никогда не достигается. Реальная ситуация соответствует полосе между этими двумя уровнями, которая на рис. 15.11 обозначена штриховкой; это означает, что достигнуть выполнения условия утечки до разрушения не так легко.
Ситуация существенным образом меняется в случае, когда сквозная трещина находится в плоском напряженном состоянии, а в рай-
Дата добавления: 2015-06-22; просмотров: 1419;
