Замечание. Для ориентированного графа петлю, т. е. дугу вида (хi, хi) удобно представлять иным значением в строке хi, например, 2.

Пример. Матричные представления графов проиллюстрированы на рис. 4.13, 4.14.

			(1,2)	(1,3)	(3,2)	(3,4)	(5,4)	(5,6)	(6,5)
			-1		-1
В=				-1
						-1	-1
									-1
								-1

Рис. 4.13:

а) ориентированный граф и его матрица инцидентности,

б) неориентированный граф и его матрица инцидентности

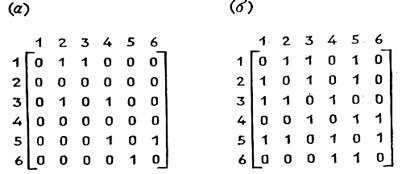
Рис. 4.14. Матрицы смежности для графов на рис. 4.13

Представление графов в ЭВМ

Очевидно, что наиболее понятный и полезный для человека способ представления графа – изображение графа на плоскости в виде точек и соединяющих их линий – будет совершенно бесполезным, если решать задачи, связанные с графами, с помощью ЭВМ. Выбор соответствующей структуры данных для представления графов имеет принципиальное влияние на эффективность алгоритмов. Рассмотрим различные способы представления графов.

В теории графов классическим способом представления графа служит матрица инцидентности. Это матрица В с n строками, соответствующими вершинам, и т столбцами, соответствующими ребрам. С алгоритмической точки зрения матрица инцидентности является, вероятно, самым худшим способом представления графа, который только можно себе представить. Во-первых, он требует п´т ячеек памяти, причем большинство этих ячеек вообще занято нулями.Неудобен также доступ к информации. Ответ наэлементарные вопросы типа «существует ли дуга (x_i, x_j) ?», «к каким вершинам ведут ребра из х_i ?»требует в худшем случае перебора всех столбцов матрицы,а следовательно, т шагов.

Лучшим способомпредставления графа является матрица смежности,определяемая как матрица А=(а_ij)размера n 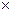n. Здесь подразумевается, что ребро (x_i, x_j) неориентированного графа идет как от x_i к x_j, так и от x_j к х_i, так что матрица смежности такого графа всегда является симметричной. Это проиллюстрировано на рис. 4.14б.

Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос «существует ли ребро из х_i в x_j?». Недостатком жеявляется тот факт, что независимо от числа ребер объем занятой памяти составляет n². На практике этонеудобство можно иногда уменьшить, храня целую строку (столбец) матрицы в одном машинном слове – это возможно для малых n.

Более экономным в отношении памяти (особенно в случае неплотных графов, когда т гораздо меньше n²)является метод представления графа с помощью списка пар, соответствующих его ребрам. Пара (x_i, x_j) соответствует дуге (x_i, x_j),если граф ориентированный, и ребру (x_i, x_j) в случае неориентированного графа (рис. 4.15). Очевидно, что объем памяти в этом случае составляет 2m. Неудобством является большое число шагов – порядка т в худшем случае, – необходимое для получения множества вершин, к которым ведут ребра из данной вершины.

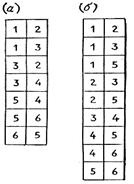
Рис. 4.15. Списки ребер, соответствующие графам на рис 4.13

Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшимрешением во многих случаях оказывается структура данных, которую называют списками инцидентности. Она содержит для каждой вершины 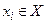список вершин x_j, таких что 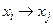(или x_i – x_j в случае неориентированного графа). Точнее, каждый элемент такого списка является записью r, содержащей вершину r.строка и указатель r.след на следующую запись в списке (r.след=nil для последней записи в списке). Начало каждого списка хранится в таблице НАЧАЛО; точнее, НАЧАЛО[x_i] является указателем на начало списка, содержащего вершины из множества (x_j: 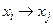)((x_j: x_i – x_j)для неориентированного графа). Весь такой список обычно неформально будем обозначать ЗАПИСЬ[x_i], а цикл, выполняющий определенную операцию для каждого элемента x_j из этого списка в произвольной, но четко установленной последовательности, соответствующей очередности элементов в списке, будем записывать «fоr x_j 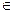ЗАПИСЬ[x_i] do ...».

Отметим, что для неориентированных графов каждое, ребро (x_j, x_i) представлено дважды: через вершину x_i в списке ЗАПИСЬ[x_j] и через вершину x_j в списке ЗАПИСЬ[x_i]. Во многих алгоритмах структура графа динамически модифицируется добавлением и удалением ребер. Каждый элемент списка может содержать указатель не только к следующему элементу, но и к предыдущему. Аналогичным способом определяем для каждой вершины x_i неориентированного графа список ПРЕДШ[x_i], содержащий вершины из множества (x_j: x_i – x_j).

Число ячеек памяти, необходимое для представления графа с помощью списков инцидентности, будет, очевидно, иметь порядок т+n. На рис. 4.16 представлены списки инцидентности, соответствующие графам на рис. 4.13.

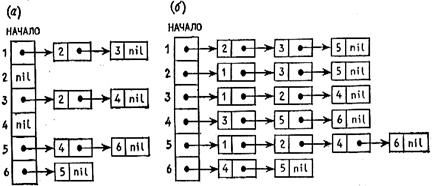
Рис. 4.16. Списки инцидентности ЗАПИСЬ,

соответствующие графам на рис. 4.13