Алгоритм нахождения сильных компонент графа можно описать следующей последовательностью шагов
Шаг 1. G = (X, V) – данный граф. Определение сильных компонент графа (СК) начать с произвольной вершины хiÎХ. Найти R(xi) и Q(xi). Положить СК(хi) = 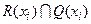 - сильная компонента графа, содержащая вершину хi.
- сильная компонента графа, содержащая вершину хi.
Шаг 2. Определить множество 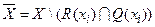 . Если
. Если 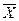 ¹Æ, то
¹Æ, то 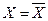 и перейти к шагу 1, иначе останов, так как все сильные компоненты определены.
и перейти к шагу 1, иначе останов, так как все сильные компоненты определены.
Граф G*=(X*,V*) определяется так: каждая его вершина представляет множество вершин некоторой сильной компоненты графа G, дуга (xi*, xj*) существует в G* тогда и только тогда, когда в G существует дуга (xi, xj), такая, что xi принадлежит компоненте, соответствующей вершине xi*, а xj –компоненте, соответствующей вершине xj*. ГрафG* называют конденсациейграфа G.
Совершенно очевидно, что конденсация G* не содержит контуров, поскольку наличие контура означает, что любые вершины этого контура взаимно достижимы. Поэтому совокупность всех вершин контура принадлежит некоторой СК в G* и, следовательно, содержится в СК графа G, что противоречит определению конденсации, в силу которого вершины из G* соответствуют СК в G.
Пример. Для графа G, приведенного на рис. 4.25, найти сильные компоненты и построить конденсацию G*.

Найдем СК в G, содержащую вершину x1.
Из соотношений (4.3) и (4.4) получаем
R(x1) ={ x1 , x2 , x4 , x5 , x6 , x7 , x8 , x9 , x10 }
Q(x1) ={ x1 , x2 , x3 , x5 , x6 }
Следовательно, СК, содержащая вершину x1, является порожденным подграфом
R(x1) 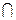 Q(x1) = ({ x1 , x2 , x5 , x6 })
Q(x1) = ({ x1 , x2 , x5 , x6 })
Аналогично, СК, содержащая вершину x8, есть порожденный подграф ({x8, x10}), СК содержащая x7 – подграф ({x4, x7, x9}), СК, содержащая x11, –подграф ({x11, x12, x13 }) и СК, содержащая x3, – подграф ({x3}). Следует отметить, что последняя СК состоит из единственной вершины графа G. Конденсация G* приведена на рис. 4.26.

Рис. 4.26. G* - конденсация графа G
Процедуру, описанную выше и связанную с нахождением СК графа, можно сделать более удобной, если непосредственно использовать матрицыR и Q. Пусть записьRÄQ означает поэлементное умножение этих матриц. Тогда сразу видно, что строка xi, матрицы RÄQ содержит единицы только в тех столбцах xj, для которых выполняется условие: вершины xi и xj взаимно достижимы; в других местах строки xi стоят нули. Таким образом, две вершины находятся в одной и той же СК тогда и только тогда, когда соответствующие им строки (или столбцы) в матрице RÄQ идентичны. Вершины, которым соответствуют строки, содержащие 1 в столбце xj, образуют множество вершин СК, содержащей xj. Отсюда мгновенно следует, что матрицу RÄQ можно преобразовать путем транспонирования строк и столбцов в блочно-диагональную. Каждая из диагональных подматриц этой матрицы соответствует СК графа G и содержит только единичные элементы, все остальные элементы блочно-диагональной матрицы равны нулю. Для приведенного ранее примера матрицаRÄQ, преобразованная соответствующим образом, имеет вид
| x1 x2 x5 x6 | x8 x10 | x4 x7 x9 | x11 x12 x13 | x3 | |
| x1 x2 x5 x6 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 | ||||
| x8 R Ä Q = x10 | 1 1 1 1 | ||||
| x4 x7 x9 | 1 1 1 1 1 1 1 1 1 | ||||
| x11 x12 x13 | 1 1 1 1 1 1 1 1 1 | ||||
| x3 |
Дата добавления: 2015-04-10; просмотров: 3730;
