Базы и антибазы

База или вершинная база В есть множество вершин графа G, из которого достижима любая вершина графа и которое является минимальным в том смысле, что не существует собственного подмножества в В, обладающего таким свойством достижимости.

Базой является такое множество вершин графа G, которое удовлетворяет следующим двум условиям:

1) каждая вершина графа G достижима хотя бы из одной вершины множества В;

2) в В нет вершины, которая достижима из другой вершины множества В.

Из этих условий получаются следующие утверждения.

1. В множестве В нет двух вершин, которые принадлежат одной и той же СК графа G.

2. В любом графе без контуров существует единственная база. Она состоит из всех таких вершин, полустепени захода которых равны 0.

Доказательства этих утверждений простые и непосредственно следуют из определений. Утверждения позволяют сформировать алгоритм нахождения баз ориентированного графа, который описывает следующая последовательность шагов.

Шаг 1. G – данный граф. Для G найти все сильные компоненты.

Шаг 2. Построить конденсацию G* графа G.

Шаг 3. Определить базу В* конденсации G*, включив в В* те вершины G*, полустепени захода которых равны 0.

Шаг 4. Построить базу В графа G из В*, взяв по одной вершине из сильных компонент, входящих в В*. Останов.

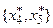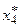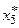Пример. Для графа G, приведенного на рис. 4.25, конденсация показана на рис. 4.26. Базой графа G* является множества , поскольку и - единственные вершины в графе G* с полустепенями захода, равными 0. Базами графа G являются 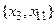, 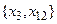и .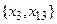

Понятие, двойственное понятию базы есть антибаза. Антибаза 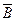графа G есть такое минимально возможное множестве вершин, что какова бы ни была вершина графа G, из нее достижима некоторая вершина в 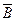. Свойства антибаз аналогичны свойствам баз, надо только «прямые» понятия заменить на двойственные. Опишем алгоритм нахождения антибаз 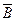графа.

Шаг 1. G - данный граф. Для G найти все сильные компоненты.

Шаг 2. Построить конденсацию G* графа G.

Шаг 3. Определить антибазу `В* конденсации G*, включив в`В* те вершины G*, полустепени исхода которых равны 0.

Шаг 4. Построить антибазу 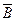графа G из `В*, взяв по одной вершине из сильных компонент, входящих в`В*. Останов.

В примере с графом G, изображенным на рис. 4.25, конденсация графа G* (рис. 4.26) содержит только одну вершину 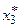с полустепенью исхода, равной 0. Таким образом, антибаза графа G* 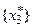, а антибазами графа G являются множества 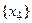, 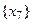и .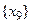

Понятия связности и достижимости применяют к исследованию структуры организаций. Например, если граф представляет структуру руководства или влияний некоторой организации, то элементы каждой сильной компоненты имеют равную власть и равное влияние друг на друга. Базу графа можно интерпретировать как «коалицию», включающую наименьшее число лиц, обладающих властью над каждым членом организации.