Независимые и доминирующие множества
Число доминирования, число независимости, кликовое число - эти числа и связанные с ними подмножества вершин описывают важные структурные свойства графа и имеют разнообразные непосредственные приложения при ведении проектного планирования исследовательских работ, в кластерном анализе, параллельных вычислениях на ЭВМ, при размещении предприятий обслуживания, а также источников и потребителей в энергосистемах. Ядро - множество вершин, которое является одновременно минимальным доминирующим и максимальным независимым, имеет важное значение в теории игр.
 Множество вершин называется независимым (внутренне устойчивым множеством), если никакие две из них не смежны. Например, для графа, изображенного на рис. 4.27, независимыми являются множества вершин: {x7, x8, x2}, {x3, x1}, {x7, x8, x2, x5}. Когда не могут возникнуть недоразумения, эти множества будут называться просто независимыми множествами (вместо независимые множества вершин).
Множество вершин называется независимым (внутренне устойчивым множеством), если никакие две из них не смежны. Например, для графа, изображенного на рис. 4.27, независимыми являются множества вершин: {x7, x8, x2}, {x3, x1}, {x7, x8, x2, x5}. Когда не могут возникнуть недоразумения, эти множества будут называться просто независимыми множествами (вместо независимые множества вершин).
Рис. 4.27
Независимое множество называется максимальным, если нет другого независимого множества, в которое оно бы входило. Для графа, изображенного на рис. 4.27, множество {x7, x8, x2, x5} является максимальным, а {x7, x8, x2} таковым не является. Следует отметить, что число элементов (вершин) в разных максимальных множествах, как следует из приведенного примера, не обязательно одинаковое.
Если Q является семейством всех максимальных независимых множеств G, то число
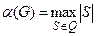
называется числом независимости графа G, а множество S*, на котором этот максимум достигается, называется наибольшим независимым множеством. Для графа на рис. 4.27 семейство максимальных независимых множеств таково: {x7, x8, x2, x5}, {x1, x3, x7}, {x2, x4, x8}, {x6, x4}, {x6, x3},{x1, x5, x7}, {x1, x4}, {x3, x7, x8}.
Наибольшее из них множество имеет 4 элемента и, следовательно, 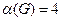 . Множество {x7, x8, x2, x5} является наибольшим независимым множеством.
. Множество {x7, x8, x2, x5} является наибольшим независимым множеством.
Пример. Пусть имеется n проектов, которые должны быть выполнены. Допустим, что для выполнения проекта xi требуется некоторое подмножество Ri наличных ресурсов из множества{1, 2, … , p}. Предположим, что каждый проект, задаваемый совокупностью средств, необходимых для его реализации, может быть выполнен за один и тот же промежуток времени. Построим граф G, каждая вершина которого соответствует некоторому проекту, а ребро (xi, xj) – наличию общих средств у проектов xi и xj, т. е. условию 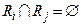 . Максимальное независимое множество вершин графа G представляет тогда максимальное множество проектов, которое можно выполнить одновременно за один и тот же промежуток времени.
. Максимальное независимое множество вершин графа G представляет тогда максимальное множество проектов, которое можно выполнить одновременно за один и тот же промежуток времени.
Реальная ситуация соответствует динамической системе, в которой происходит постоянное обновление проектов через определенный промежуток времени. Поэтому каждый раз надо заново повторять процедуру построения максимального независимого множества в соответствующем графа G. В практических ситуациях бывает весьма не просто выполнить множество проектов, соответствующих максимальному независимому множеству на данном отрезке времени, поскольку исполнение некоторых проектов может быть по каким-то причинам отложено. Тогда лучший способ действия состоит в присвоении каждому проекту (вершине) xi некоторого штрафа рi, который увеличивается с ростом времени отсрочки в исполнении проекта. В каждый расчетный момент времени надо выбирать из семейства максимальных независимых множеств такое множество, которое максимизирует некоторую функцию штрафа на вершинах, содержащихся в выбранном множестве.
Множество ребер называется независимым, если никакие два из них не смежны. Наибольшее число ребер в независимом множестве ребер называется реберным числом независимости и обозначается β1. Для полного графа с четным числом вершин β1(К2n)=n, для полного графа с нечетным числом вершин β1(К2n+1)=n–1. Независимое множество ребер называется также паросочетанием.
Независимость тесно связана с понятием доминирования.
Для графа G=(X,V) множество вершин D⊆Х называется доминирующим множеством (внешне устойчивым множеством), если 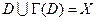 , то есть для каждой вершины xj∉D существует дуга, идущая из некоторой вершины xi∈D в xj.
, то есть для каждой вершины xj∉D существует дуга, идущая из некоторой вершины xi∈D в xj.
Доминирующее множество называется минимальным, если его подмножество не является доминирующим. Как и в случае максимальных независимых множеств, в графе может быть несколько минимальных доминирующих множеств, и они не обязательно содержат одинаковое число вершин. Доминирующее множество называется наименьшим, если число элементов в нем минимально. К задачам такого типа относят, например, следующие:
1) Размещение телевизионных или радиопередающих станций на некоторой территории.
2) Размещение центров торговли обслуживающих некоторые районы.
Теорема 4.9.1. Независимое множество вершин является максимальным тогда и только тогда, когда оно является доминирующим.
4.9.1. Нахождение всех максимальных независимых множеств
Задача отыскания экстремальных независимых и покрывающих множеств возникает во многих практических случаях. Например, пусть есть множество процессов, использующих неразделяемые ресурсы. Соединим ребрами вершины, соответствующие процессам, которым требуется один и тот же ресурс. Тогда β0 будет определять количество возможных параллельных процессов.
Примером задачи, в которой требуется отыскать максимальные независимые множества, является известная задача о восьми ферзях: расставить на шахматной доске 8 ферзей так, чтобы они не били друг друга. Для решения достаточно представить доску в виде графа с 64 вершинами (соответствующими клеткам доски), которые смежны, если клетки находятся на одной вертикали, горизонтали или диагонали.
Нахождение всех максимальных независимых множеств можно осуществить последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (путем добавления к исследуемому множеству дополнительной, не принадлежащей ему вершины и выяснением того, сохраняется ли независимость) и запоминанием максимальных множеств. С увеличением числа вершин этот метод поиска становится с вычислительной точки зрения громоздким, поэтому его удобно использовать только для небольших графов, например, с числом вершин, не превосходящих 20. Однако число максимальных независимых множеств увеличивается, но при выполнении процедуры большое число независимых множеств формируется, а затем вычеркивается, так как обнаруживается, что они содержатся в других, ранее полученных множествах, и поэтому не являются максимальными.
Используем систематический метод перебора Брона и Кэрбоша [2], который позволяет обходить указанные трудности. В этом методе не нужно запоминать генерируемые независимые множества для проверки их на максимальность путем сравнения с ранее сформированными множествами.
Введем необходимые обозначения обоснуем алгоритм нахождения всех максимальных независимых множеств.
В процессе поиска - на некотором этапе k - независимое множество вершин Sk расширяется путем добавления к нему подходящим образом выбранной вершины (чтобы получилось новое независимое множество Sk+1) на этапе k+1, и так поступают до тех пор, пока добавление вершин станет невозможным, а порожденное множество не станет максимально независимым множеством. Пусть Qk будет на этапе k наибольшим множеством вершин, для которого Sk∩Qk=Æ, то есть после добавления любой вершины из Qk в Sk получится независимое множество Sk+1. В некоторый произвольный момент работы алгоритма множество Qk состоит из вершин двух типов: подмножества Qk- тех вершин, которые уже использовались в процессе поиска для расширения множества Sk, и подмножества Qk+ таких вершин, которые еще не использовались. Тогда дальнейшее ветвление в дереве поиска включает процедуру выбора вершины xikÎQk+, добавления ее к Sk
Sk+1 = SkÈ{xik}
и порождения новых множеств:
Qk-+1 = Qk- \ Г(xik);
Qk++1 = Qk+ \ (Г(xik) È {xik}).
Шаг возвращения алгоритма состоит в удалении вершины xik из Sk+1, чтобы вернуться к Sk, изъятии xik из старого множества Qk+ и добавлении xik к старому множеству Qk- для формирования новых множеств Qk- и Qk+.
Множество Sk является максимально независимым множеством только тогда, когда невозможно его дальнейшее расширение, то есть когда Qk+=Æ. Если Qk-¹Æ, то текущее множество Sk было расширено на некотором предшествующем этапе работы алгоритма путем добавления вершины из Qk-, и поэтому не является максимальным независимым множеством. Таким образом, необходимым и достаточным условием того, что Sk - максимально независимое множество, является выполнение равенств:
Qk+ = Qk- = Æ.
Если очередной этап работы алгоритма наступает тогда, когда существует некоторая вершина xÎQk-, для которой Г(x)ÇQk+=Æ, то безразлично, какая из вершин, принадлежащих Qk+, использовалась для расширения Sk, и это справедливо при любом числе дальнейших ветвлений. Вершина x не может быть удалена из Qp- на любом следующем шаге p > k. Таким образом, существование x, такого что
хÎQk- и Г(x)ÇQk+ = Æ (4.5)
является достаточным для применения шага возвращения, потому что из Sk при всяком дальнейшем ветвлении уже не получится максимально независимое множество.
Если k=0, то возвращение выполнить невозможно, поэтому при k=0 осуществляется переход на прямой шаг.
Опишем алгоритм нахождения всех максимальных независимых множеств вершин графа.
Начальная установка.
Шаг 1.Пусть S0 = Q0- = Æ, Q0+= X, k=0.
Прямой шаг.
Шаг 2.Выбрать вершину xikÎQk+ и сформировать Sk+1, Qk-+1 и Qk++1, оставив Qk- и Qk+ нетронутыми. Положить k=k+1.
Проверка.
Шаг 3.Если выполняется условие (4.5), то перейти к шагу 5 иначе к шагу 4.
Шаг 4. Если Qk+=Qk- =Æ, то напечатать максимальное независимое множество Sk и перейти к шагу 5. Если Qk+=Æ, а Qk-¹Æ, то перейти к шагу 5, иначе - к шагу 2.
Шаг возвращения.
Шаг 5.Положить k=k–1. Удалить xik из Sk+1, чтобы получить Sk. Исправить Qk+ и Qk-, удалив вершину xik из Qk+ и добавив ее к Qk-. Если k¹0, то перейти к шагу 3, иначе если Q0+=Æ, то остановиться (к этому моменту будут напечатаны все максимальные независимые множества), иначе перейти к шагу 2.
 Пример. Найти все максимальные независимые множества графа G.
Пример. Найти все максимальные независимые множества графа G.
Матрица смежности графа G:
| А= | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 |
1. Начальная установка:
S0 = Ø; Q0- = Ø; Q0+ = {x1, x2, x3, x4, x5, x6, x7}; k=0.
2. Прямой шаг:
x1; S1 = {x1}; Q1- = Ø; Q1+ = {x4, x5, x6, x7}; k = 1.
3. Проверка.
Условие не выполняется, переходим к шагу 4 (→ 4).
4. Условие не выполняется → 2.
2. x4; S2 = {x1, x4}; Q2- = Ø; Q2+ = {x7}; k = 2.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x7; S3 = {x1, x4, x7}; Q3- = Ø; Q3+ = Ø; k = 3.
3. Условие не выполняется → 4.
4. S3 = {x1, x4, x7} - максимальное независимое множество → 5.
5. k = 2; S2 = {x1, x4}; Q2- = {x7}; Q2+ = Ø → 3.
3. Условие выполняется → 5.
5. k = 1; S1 = {x1}; Q1- = {x4}; Q1+ = {x5, x6, x7} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x5; S2 = {x1, x5}; Q2- = Ø; Q2+ = {x6}; k = 2.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x6; S3 = {x1, x5, x6}; Q3- = Ø; Q3+ = Ø; k = 3.
3. Условие не выполняется → 4.
4. S3 = {x1, x5, x6} - максимальное независимое множество → 5.
5. k = 2; S2 = {x1, x5}; Q2- = {x6}; Q2+ = Ø → 3.
3. Условие выполняется → 5.
5. k = 1; S1 = {x1}; Q1- = {x4, x5}; Q1+ = {x6, x7} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x6; S2 = {x1, x6}; Q2- = {x5}; Q2+ = Ø; k = 2.
3. Условие выполняется → 5.
5. k = 1; S1 = {x1}; Q1- = {x4, x5, x6}; Q1+ = {x7} → 3.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1}; Q0+ = {x2, x3, x4, x5, x6, x7} → 2.
2. x2; S1 = {x2}; Q1- = Ø; Q1+ = {x3, x5, x7}; k = 1.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x3; S2 = {x2, x3}; Q2- = Ø; Q2+ = Ø; k = 2.
3. Условие не выполняется → 4.
4. S2 = {x2, x3} — максимальное независимое множество → 5.
5. k = 1; S1 = {x2}; Q1- = {x3}; Q1+ = {x5, x7} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x5; S2 = {x2, x5}; Q2- = Ø; Q2+ = Ø; k = 2.
3. Условие не выполняется → 4.
4. S2 = {x2, x5} — максимальное независимое множество → 5.
5. k = 1; S1 = {x2}; Q1- = {x3, x5}; Q1+ = {x7} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x7; S2 = {x2, x7}; Q2- = Ø; Q2+ = Ø; k = 2.
3. Условие не выполняется → 4.
4. S2 = {x2, x7} — максимальное независимое множество → 5.
5. k = 1; S1 = {x2}; Q1- = {x3, x5, x7}; Q1+ = Ø → 3.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2}; Q0+ = {x3, x4, x5, x6, x7} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x3; S1 = {x3}; Q1- = {x2}; Q1+ = {x4, x6}; k = 1.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x4; S2 = {x3, x4}; Q2- = Ø; Q2+ = Ø; k = 2.
3. Условие не выполняется → 4.
4. S2 = {x3, x4} — максимальное независимое множество → 5.
5. k = 1; S1 = {x3}; Q1- = {x2, x4}; Q1+ = {x6} → 3.
3. Условие не выполняется → 4.
4. Условие не выполняется → 2.
2. x6; S2 = {x3, x6}; Q2- = Ø; Q2+ = Ø; k = 2.
3. Условие не выполняется → 4.
4. S2 = {x3, x6} — максимальное независимое множество → 5.
5. k = 1; S1 = {x3}; Q1- = {x2, x4, x6}; Q1+ = Ø → 3.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2, x3}; Q0+ = {x4, x5, x6, x7} → 2.
2. x4; S1 = {x4}; Q1- = {x1, x3}; Q1+ = {x7}; k = 1.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2, x3, x4}; Q0+ = {x5, x6, x7} → 2.
2. x5; S1 = {x5}; Q1- = {x1, x2}; Q1+ = {x6}; k = 1.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2, x3, x4, x5}; Q0+ = {x6, x7} → 2.
2. x6; S1 = {x6}; Q1- = {x1, x3, x5}; Q1+ = Ø; k = 1.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2, x3, x4, x5, x6}; Q0+ = {x7} → 2.
2. x7; S1 = {x7}; Q1- = {x1, x2, x4}; Q1+ = Ø; k = 1.
3. Условие выполняется → 5.
5. k = 0; S0 = Ø; Q0- = {x1, x2, x3, x4, x5, x6, x7}; Q0+ = Ø → останов.
Таким образом, данный граф имеет семь максимальных независимых множеств:
S1 = {x1, x4, x7}; S2 = {x1, x5, x6}; S3 = {x2, x3}; S4 = {x2, x5}; S5 = {x2, x7}; S6 = {x3, x4}; S7 = {x3, x6}.
Ядро - множество, которое является одновременно минимальным доминирующим и максимальным независимым.
Утверждение 4.9.1. Конечный граф без петель, не содержащий контуров нечетной длины, обладает ядром.
Понятие, противоположное максимальному независимому множеству, есть максимальный полный подграф. Максимальный полный подграф графа G называется кликой графа. Следовательно, в противоположность максимальному независимому множеству, в котором не могут встретиться две смежные вершины, в клике все вершины попарно смежны. Совершенно очевидно, что максимальное независимое множество графа G соответствует клике графа 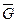 и наоборот, где
и наоборот, где 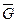 – дополнение графа G.
– дополнение графа G.
Кликовое число – максимальное число вершин в кликах данного графа.
Утверждение. 4.9.2. Максимальное независимое множество графа G соответствует клике графа `G и наоборот.
Дата добавления: 2015-04-10; просмотров: 3607;
