Нахождение сильных компонент

Сильная компонента (СК) графа G определяется как максимальный сильно связный подграф графа G. Поскольку в сильно связном графе произвольная вершина x_j достижима из любой другой вершины x_i, то в ориентированном графе существует одна и только одна СК, содержащая данную вершину x_i. В самом деле, если бы вершина x_i, принадлежала двум или большему числу сильных компонент, то существовал бы путь из любой вершины одной СК в произвольную вершину другой СК и, следовательно, объединение этих сильных компо­нент было бы сильно связным графом, что противоречит опре­делению СК.

Если вершина x_i, одновременно является начальной и конечной вершиной пути, то множество вершин, существенных относительно этих двух идентичных концов (т.е. множество вершин некоторого цикла, содержащего x_i), совпадает с пересечением 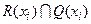. Поскольку все эти существенные вершины достижимы из x_i и, кроме того, из каждой такой вершины достижима вершина x_i, то все они взаимно достижимы. Более того, если нет другой вершины, существенной относительно концов x_i и x_i, то множество 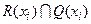, которое может быть построено с использованием соотношений (4.3) и (4.4), однозначно определяет СК графа G, содержащую вершину x_i.

Если эти вершины удалить из графа G=(X,V), то в оставшемся порожденном подграфе 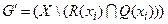можно таким же способом выделить новую СК, содержащую x_jÎ 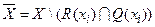. Эту процедуру можно повторять до тех пор, пока все вершины графа G не будут сгруппированы в соответствующие СК. После завершения этой процедуры граф G будет разбит на свои сильные компоненты.