И контрдостижимостей

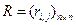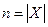Матрица достижимостей графа G=(X,V) , определяется следующим образом:

Множество вершин R(x_i) графа G, достижимых из заданной вершины x_i, состоит из таких элементов x_j, для которых (i, j)-й элемент в матрице достижимостей равен 1. Считают, что каждая вершина достижима из себя самой с помощью пути длины 0, поэтому все диагональные элементы в матрице R равны 1.

Поскольку Г(x_i) является множеством таких вершин x_j, которые достижимы из x_i c использованием путей длины 1 (т.е. Г(x_i) – такое множество вершин, для которых в графе суще­ствуют дуги (x_i, x_j)) и поскольку Г(x_j) является множеством вершин, достижимых из x_j с помощью путей длины 1, то множество Г(Г(x_i))=Г²(x_i) состоит из вершин, достижимых из x_i c использованием путей длины 2. Аналогично Г^p(x_i) является множеством вершин, которые достижимы из x_i с помощью путей длины р.

Так как любая вершина графа G, которая достижима из x_i, должна быть достижима с использованием пути (или путей) дли­ны 0, или 1, или 2, ..., или р (с некоторым конечным р≤n), то множество вершин, достижимых из x_i , можно представить в виде

R(x_i) = { x_i }ÈГ(x_i)È Г² (x_i )È…È Г^p (x_i ) (4.3)

Таким образом, множество R(x_i) может быть получено последова­тельным выполнением (слева направо) операций объединения в соотношении (4.3), до тех пор, пока «текущее» множество не перестанет изменяться при очередной операции объединения. С этого момента последующие операции не будут давать новых элементов множеству и, таким образом, будет получено, достижимое множество R(x_i). Число объединений, которое нужно выполнить, зависит от графа, но, очевидно, что число р меньше числа вершин в графе.

Матрицу достижимостей можно построить так. Находим достижимые множества R(x_i) для всех вершин x_iÎХ способом, приведенным выше. Положим r_ij=1, если x_jÎR(x_i), и r_ij=0 в противном случае. Полученная таким образом матрица R является матрицей достижимостей.

Матрица контрдостижимостей (матрица обратных достижимостей) 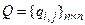, 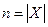определяется следующим образом:

Контрдостижимым множеством Q(x_i) графа G является множество таких вершин, что из любой вершины этого множества можно достигнуть вершину x_i. Аналогично построению достижимого множества R(x_i) на основе соотношения (4.3) можно «сформиро­вать» множество Q(x_i), используя следующее выражение:

Q(x_i) = {x_i} È Г^-1 (x_i) È Г^-2 (x_i) È … È Г^-р (x_i), (4.4) где Г^-2 (x_i) = Г^-1 (Г^-1 (x_i)) и т. д.

Операции, выполняются слева направо до тех пор, пока очередная операция объединения не перестанет изменять «текущее» множе­ство Q(x_i).

Из определений очевидно, что столбец x_i матрицы Q (в котором q_ij=1, если x_iÎQ(x_i), и q_ij=0 в противном случае) совпадает со строкой x_i матрицыR,т. е.Q=R^T, гдеR^T– матрица, транспонированная к матрице достижимостей R.

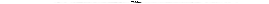Пример. Найти матрицы достижимостей и обратных достижимостей для графа G, приведенного на рис. 4.24.

Рис.4.24

Матрица смежности графа G имеет вид

Множества достижимостей находятся с помощью соотношений

R(x₁)={x₁} È {x₂,x₅} È {x₂,x₄,x₅} È {x₂,x₄,x₅} = {x₁,x₂,x₄,x₅},

R(x₂)= {x₂} È {x₂,x₄} È {x₂,x₄,x₅} È {x₂,x₄,x₅} = {x₂,x₄,x₅},

R(х₃)= {x₃} È {x₄} È {x₅} È {x₅} = {x₃,x₄,x₅},

R(х₄)= {x₄} È {x₅} È {x₅} = {x₄,x₅},

R(х₅)= {x₅} È {x₅} = {x₅},

R(х₆)= {x₆} È {x₃,x₇} È {x₄Èx₆} È {x₃,x₅,x₇} È {x₄,x₅,x₆}=

= {x₃,x₄,x₅,x₆,x₇},

R(х₇)= {x₇} È {x₄,x₆} È {x₃,x₅,x₇} È {x₄,x₅,x₆}=

= {x₃,x₄,x₅,x₆,x₇}.

Следовательно, матрица достижимостей имеет вид

матрица обратных достижимостей такова:

Так как R(x_i) является множеством вершин, достижимых из x_i, а Q(x_j)– множеством вершин, из которых можно достиг­нуть x_j, то 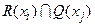– множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от x_i к x_j. Эти вершины называются существенными или неотъем­лемыми относительно двух концевых вершин x_i и x_j. Все остальные вершины 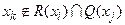называются несуществен­ными или избыточными, поскольку их удаление не влияет на пути от x_i к x_{j .}

Матрицы достижимостей и обратных достижимостей являются полными в том смысле, что на длины путей от x_i к x_j не накладывались никакие ограничения. С другой стороны, можно определить матрицы ограниченных достижимостей и контрдостижимостей – надо потребовать, чтобы длины путей не превышали некоторого заданного числа. Эти ограниченные матрицы тоже могут быть построены с помощью соотношений (4.3) и (4.4) – надо действовать точно так, как раньше, при нахожде­нии «неограниченных» матриц, но только теперь р будет верхней границей длины допустимых путей.

Для неориентированного графа множество достижимости позволяет проверить граф на связность. Опишем алгоритм проверки связности неорграфа.

Шаг 1. G =(X,V) – данный неорграф. Для произвольной вершины х_iÎХ найти множество R(x_i). Перейти к шагу 2.

Шаг 2. Если R(x_i)=X, то граф является связным, иначе граф не является связным. Выдать соответствующее сообщение. Останов.