Основные определения. Понятия связности и достижимости используются для исследования структур различных организаций

Понятия связности и достижимости используются для исследования структур различных организаций. Например, систему связи любой организации можно интерпретировать как граф, в котором люди представлены вершинами, а каналы связи – дугами. Естественно при рассмотрении такой системы поставить вопрос, может ли информация от одного лица x_i быть передана другому лицу х_j, т. е. существует ли путь, идущий от вершины x_i к вершине х_j. Если в графе существует путь, идущий от вершины x_i к вершине х_j, то говорят, что вершина x_jдостижима из вершины х_i.

Если для любой пары вершин неориентированного графа существует цепь их соединяющая, то такой граф называетсясвязным. Иначе неориентированный граф называетсянесвязным.

Ориентированный граф называется сильно связным или сильным, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь, соединяющий x_i с x_j. Это определение означает также, что любые две вершины такого графа взаимно достижимы.

Ориентированный граф называется односторонне связным или односторонним, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь из x_i в x_j или из x_j в x_i (или оба одновременно).

Ориентированный граф называют слабо связным или слабым, если для любых двух различных вершин графа существует по крайней мере один маршрут, соединяющий их.

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязным.

Маршрут есть неориентированный двойник пути. Маршрут позволяет осуществлять «движение» по дугам, без учета их направленности.

Пример. Граф, приведенный на рис. 4.23(а) является сильно связный. Граф, показанный на рис. 4.23(б), не является сильным, так как в нем нет пути из x₅ в x₂, но односторонне связный. Граф, изображенный на рис. 4.23(в), не является ни сильным, ни односторонним, поскольку в нем не существует путей от x₅ к x₂ и от x₂ к x₅. Он – слабо связный. Наконец, граф, приведен­ный на рис. 4.23(г), является несвязным.

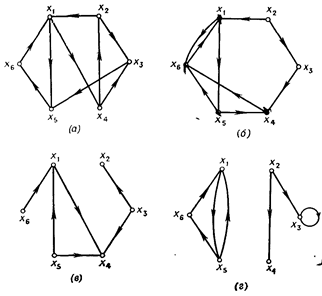
Рис. 4.23. Сильно связный граф (а), односторонне связный граф (б), слабо связный граф (в), несвязный граф (г)

Пусть дано некоторое свойство Р, которым могут обладать графы. Максимальным подграфом графа G относительно свойства Р называется порожденный подграф (X_S) графа G, обладающий этим свойством и такой, что не существует другого порожденного подграфа (Х_H), у которого X_SÌX_H и который также обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связность, то максимальным сильным подграфом графа G является сильный подграф, который не содержится в любом другом сильном подграфе, такой подграф называется сильной компонентой графа G. Это определения можно дать так: всякий максимальный по включению сильно связный подграф данного графа называется его сильной компонентой связности. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента - максимальный слабый подграф.

Например, в графе G, приведенном на рис. 4.23(6), подграф ({х₁, x₄, х₅, х₆}) является сильной компонентой графа G. С другой стороны, подграфы ({х₁, х₆}) и ({х₁, х₅, х₆}) не являются сильными компонентами, хотя и являются сильными подграфами, поскольку они содержатся в графе ({х₁, x₄, x₅, х₆}) и, следова­тельно, не максимальные. В графе, показанном на рис. 4.23(в), подграф ({x₁, x₄, х₅}) является односторонней компонентой. В графе, приведенном на рис. 4.23(г), оба подграфа ({х₁, х₅, х₆}) и ({х₂, х₃, x₄}) являются слабыми компонентами, и у этого графа только две такие компоненты.

Из определений сразу же следует, что односторонние компоненты графа могут иметь общие вершины. Сильная компонента должна содержаться по крайней мере в одной односторонней компоненте, а односторонняя компонента содержится в некоторой слабой компоненте данного графа G.

Максимальный связный подграф неориентированного графа G называетсякомпонентой связности.

Максимальный сильно связный подграф ориентированного графа G называется сильной компонентой связности (СК).

Существуют два вида связности – вершинная связность и реберная связность.Число вершинной связности– это наименьшее число вершин, удаление которых (вместе с инцидентными ребрами) приводит к несвязному графу.Число реберной связности– это наименьшее число ребер, удаление которых приводит к несвязному графу. При исследовании коммуникационных и логических сетей числа связности соответствующих графов можно интерпретировать как степень надежности этих сетей.