Алгоритм построения остова неорграфа
Замечание. Процедура основана на просмотре в произвольном порядке ребер исходного графа и может быть представлена как процесс окрашивания их. При этом синий цвет используется для окраски ребер, включаемых в остов, а красный – для окраски ребер, не включаемых в остов. При рассмотрении ребра осуществляется проверка того, не образует ли данное ребро в совокупности с ребрами, уже включенными в остов, цикл. Эта проверка осуществляется следующим образом. Ребра, включенные в остов, составляют граф, имеющий одну или несколько компонент связности. Вершины, принадлежащие отдельно взятой компоненте, объединяются в совокупность, которую будем называть «букетом». Некоторое ребро образует цикл с ребрами, уже включенными в остов, если обе его концевые вершины принадлежат одному и тому же букету.
Результаты работы алгоритма удобно записывать в таблицу:
| ребро | цвет | букет 1 | букет 2 | … | … |
Шаг 1. Выбрать любое ребро, не являющееся петлей. Окрасить его в синий цвет и сформировать букет, включив в него концевые вершины окрашенного ребра.
Шаг 2. Выбрать любое неокрашенное ребро, не являющееся петлей. Если в графе такого ребра нет, то останов. Исходный граф не содержит остова. Иначе перейти к шагу 3.
Шаг 3. а) Если обе концевые вершины выбранного ребра принадлежат одному букету, то окрасить выбранное ребро в красный цвет.
б) Если одна из концевых вершин выбранного ребра принадлежит некоторому букету, а другая концевая вершина не принадлежит ни одному букету, то окрасить выбранное ребро в синий цвет и включить его концевую вершину, не принадлежавшую ранее ни одному букету, в тот же букет, которому принадлежит другая концевая вершина рассматриваемого ребра.
в) Если ни одна из концевых вершин не принадлежит ни одному букету, то окрасить рассматриваемое ребро в синий цвет и сформировать новый букет из его концевых вершин.
г) Если концевые вершины выбранного ребра принадлежат различным букетам, то окрасить ребро в синий цвет, а оба букета, которым принадлежат его концевые вершины, соединить в один букет.
Шаг 4. Если все вершины графа вошли в один букет, то останов - синие ребра образуют остов. Иначе перейти к шагу 2.
Также существуют алгоритмы порождения всех остовных деревьев произвольного неориентированного графа. В некоторых ситуациях возникает необходимость в построении полного списка остовных деревьев графа G. Например, в том случае, когда надо отобрать «наилучшее» дерево, а критерий, позволяющий осуществить такой отбор, является очень сложным (или даже частично субъективным), так что непосредственное решение задачи оптимизации (не использующее перечисление всех остовных деревьев) оказывается невыполнимым.
 Поскольку число остовых деревьев графа очень быстро растет с ростом числа его ребер, то, очевидно, нужен эффективный метод порождения исчерпывающего, но без повторений, списка остовых деревьев. Один из таких способов состоит в использовании элементарных преобразований деревьев для последовательного порождения остовов, начиная с некоторого начального остова Т0. Методы, основанные на этом принципе, даны в работах Пауля, Чена и других. Однако процедурам, опирающимся на элементарные преобразования деревьев, присущ следующий недостаток: для порождения нового элемента дерева необходимо привлекать все найденные ранее деревья. Очевидно, что наилучшим будет такой алгоритм порождения всех остовов графа, когда список остовов строится без повторений и построенные остовы записываются во вспомогательную память, но в процессе работы алгоритма из этой памяти ничего не берется. В [2] описан такой алгоритм.
Поскольку число остовых деревьев графа очень быстро растет с ростом числа его ребер, то, очевидно, нужен эффективный метод порождения исчерпывающего, но без повторений, списка остовых деревьев. Один из таких способов состоит в использовании элементарных преобразований деревьев для последовательного порождения остовов, начиная с некоторого начального остова Т0. Методы, основанные на этом принципе, даны в работах Пауля, Чена и других. Однако процедурам, опирающимся на элементарные преобразования деревьев, присущ следующий недостаток: для порождения нового элемента дерева необходимо привлекать все найденные ранее деревья. Очевидно, что наилучшим будет такой алгоритм порождения всех остовов графа, когда список остовов строится без повторений и построенные остовы записываются во вспомогательную память, но в процессе работы алгоритма из этой памяти ничего не берется. В [2] описан такой алгоритм.
Пример. Для графа, изображенного на рис. 4.32, все остовные деревья приведены на рис. 4.33.
Рис. 4.32
Легко проверить, что у графа, изображенного на рис. 4.32, действительно 21 остов.

1 2 3 4 5 6 7
8 9 10 11 12 13 14

15 16 17 18 19 20 21
Рис. 4.33. Все остовы графа, изображенного на рис. 4.32
4.11.3. Кратчайшие остовы
Иногда дугам графа G сопоставляются (приписываются) числа - дуге (хi, хj) ставится в соответствие некоторое число 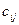 называемое весом, длиной или стоимостью (ценой) дуги. Тогда граф G называется графом со взвешенными дугами. Иногда веса (числа
называемое весом, длиной или стоимостью (ценой) дуги. Тогда граф G называется графом со взвешенными дугами. Иногда веса (числа 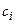 ) приписываются вершинам хi графа, и тогда получается граф со взвешенными вершинами. Если в графе веса приписаны и дугам, и вершинам, то он называется просто взвешенным.
) приписываются вершинам хi графа, и тогда получается граф со взвешенными вершинами. Если в графе веса приписаны и дугам, и вершинам, то он называется просто взвешенным.
 |
При рассмотрении пути
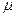 , представленного последовательностью дуг (v1, v2,. . ., vq),за его вес (длину, стоимость) принимается число l(
, представленного последовательностью дуг (v1, v2,. . ., vq),за его вес (длину, стоимость) принимается число l( 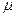 ), равное сумме весов всех дуг, входящих в
), равное сумме весов всех дуг, входящих в 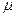 , т. е.
, т. е.
Таким образом, когда слова «длина», «стоимость», «цена» и «вес» применяются к дугам, то они эквивалентны по содержанию, и в каждом конкретном случае выбирается такое слово, которое ближе подходит по смыслу и совпадает с принятым в литературе. Длиной (или мощностью) пути 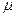 называется число дуг, входящих в него.
называется число дуг, входящих в него.
Опишем алгоритмы нахождения остова минимального веса во взвешенном графе, т. е. кратчайшего остова. Эта задача возникает при проектировании линий электропередач, дорог и т. п., когда требуется заданные центры (вершины) соединить некоторой системой каналов связи (ребер) так, чтобы любые два центра были связаны либо непосредственно соединяющим их каналом (ребром), либо через другие центры и каналы, т. е. цепью, и чтобы общая длина (или, например, стоимость) каналов связи была минимальной. Искомая сеть будет остовом минимального веса полного графа.
В любом связном графе существует остов, причем в общем случае он может быть выделен не единственным способом. Существует несколько алгоритмов для определения кратчайшего остова (сумма весов ребер остова минимальна).
Рассмотрим алгоритм Прима построениякратчайшего остова взвешенного графа.
Шаг 1. Рассмотрим граф 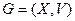 с матрицей весов
с матрицей весов 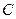 (матрица смежности, в которой элементы, индексы которых соответствуют смежным вершинам, равны не единице, а весу соответствующего ребра). Множество вершин остова положим
(матрица смежности, в которой элементы, индексы которых соответствуют смежным вершинам, равны не единице, а весу соответствующего ребра). Множество вершин остова положим 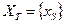 ,
, 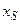 - произвольно выбранная вершина. А множество ребер
- произвольно выбранная вершина. А множество ребер 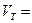 Æ.
Æ.
Шаг 2. Для каждой вершины 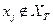 найти вершину
найти вершину 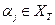 , такую, что
, такую, что 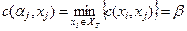 . И приписать вершине хj пометку [
. И приписать вершине хj пометку [ 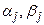 ]. Если такой вершины нет, т.е.
]. Если такой вершины нет, т.е. 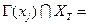 Æ, то приписать вершине
Æ, то приписать вершине 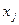 пометку [0,
пометку [0, 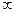 ]. Перейти к шагу 3.
]. Перейти к шагу 3.
Шаг 3. Выбрать вершину 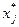 , такую, что
, такую, что 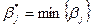 , и положить множество
, и положить множество  и
и 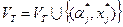 . Если
. Если 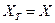 , то останов – ребра в множестве
, то останов – ребра в множестве 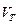 образуют кратчайший остов, иначе перейти к шагу 4.
образуют кратчайший остов, иначе перейти к шагу 4.
Шаг 4. Для всех вершин 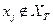 и таких, что
и таких, что 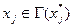 обновить пометки следующим образом: если
обновить пометки следующим образом: если 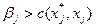 , то
, то 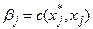 ,
, 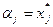 . Перейти к шагу 3.
. Перейти к шагу 3.
Рассмотрим работу алгоритма на примере. Пусть дан взвешенный граф 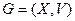 (рис. 4.34).
(рис. 4.34).
 |
Рис. 4.34. Граф 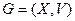
Полагаем 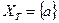 и
и 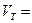 Æ. Формируем пометки для вершин.
Æ. Формируем пометки для вершин.
b [a,5], e [a,14], f [a,8], c [0, 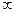 ], d [0,
], d [0, 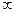 ].
].
Выбираем вершину с минимальной пометкой, т.е. вершину b. Добавляем эту вершину к 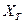 , а соответствующее ребро к
, а соответствующее ребро к 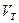 .
.
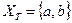 ,
, 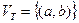 .
.
Меняем пометки для вершин, смежных с вершинами из множества 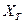 . Пометку вершины e [a,14] меняем на [b,7].
. Пометку вершины e [a,14] меняем на [b,7].
c [b,10], e [b,7], f [a,8], d [0, 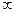 ].
].
Выбираем вершину с минимальной пометкой, т.е. вершину e, формируем множества 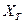 и
и 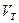 .
.
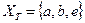 ,
, 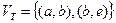 .
.
Устанавливаем пометки вершин.
f [e,3], d [e,20], c [b,10]. Вершина с минимальной помет-кой - f.
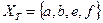 ,
, 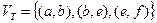 и т.д.
и т.д.
c [b,10], d [e,20]. Вершина с минимальной пометкой - c.
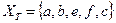 ,
, 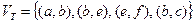
d [c,12].
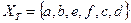 ,
,
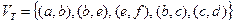
Т.к. 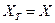 , то все вершины включены в остов, останов алгоритма. Кратчайший остов представлен на рис. 4.35.
, то все вершины включены в остов, останов алгоритма. Кратчайший остов представлен на рис. 4.35.

Рис. 4.35
Рассмотрим алгоритм Краскала построения кратчайшего остова взвешенного графа.
Шаг 1. Включить в остов T все вершины исходного графа. Пусть количество вершин равно n.
Шаг 2. Упорядочить ребра графа G в порядке неубывания из весов.
Шаг 3. Начав с первого ребра в этом списке, добавлять ребра в граф Т, соблюдая условие: такое добавление не должно приводить к появлению цикла в графе Т.
Шаг 4. Повторять шаг 3 до тех пор, пока число ребер в Т не станет равным n-1. Полученный граф Т является кратчайшим остовом графа G.
 Приведенный алгоритм, в частности, позволяет находить остов в невзвешенном графе, положив сij = 1 для всех ребер.
Приведенный алгоритм, в частности, позволяет находить остов в невзвешенном графе, положив сij = 1 для всех ребер.
Пример. На рис. 4.36 показан остов минималь-ного веса взвешенного графа. Ребра, вошедшие в остов, выделены жир-ным. Вес остова равен 9.
Дата добавления: 2015-04-10; просмотров: 2855;
