Алгоритм Durbin'а

Воспользуемся блочным представлением матрицы 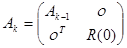, 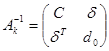. Переходя к блокам в матричном равенстве 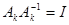, получим: 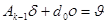, 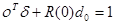. Теперь

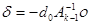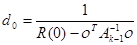, (2)

Представим вектор 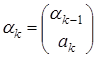. Теперь 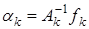= 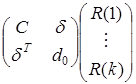. Имеем 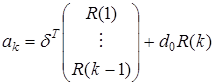. Применяя (2), получим 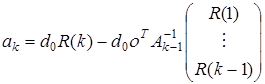. По определению 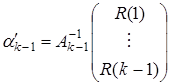есть решение аналогичной задачи, но для случая числа коэффициентов 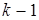. Используя явный вид выражения для 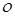, получим

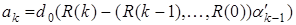(3)

Далее 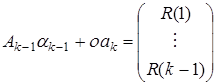. Это означает, что 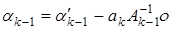. Осталась задача подсчета 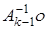, входящего также в формулу (2). Этот вектор является решением системы 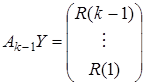. Переставляя в этой системе строки и столбцы, записывая их в обратном порядке, получим, что 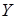получается из вектора 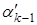записыванием компонентов в обратном порядке.

Величина 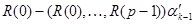, стоящая в знаменателе для подсчета 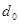, имеет следующий содержательный смысл: это 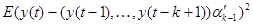. При доказательстве используются соотношения (1).