Аналог фильтра с конечным временем отклика для преобразования Адамара.

Рассмотрим матрицу Адамара 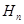. Для строк этой матрицы определена операция поэлементного перемножения строк. По индукции проверяется замкнутость. В результате получаем диадическую группу. На этой группе заданы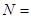 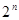характеров: 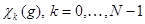Каждый характер - столбец матрицы. Характер обладает свойством: 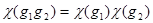. Характеры ортогональны, и любая функция на группе раскладывается по характерам.

Пусть исходный сигнал задан в 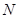точках. Можем считать, что он задан функцией 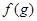на строках 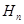. Функция раскладывается по характерам группы: 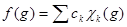. В силу симметрии матрицы, это обычное преобразование Адамара, а коэффициенты разложения составляют спектр. Выберем натуральное 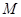, элементы группы 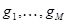и числа 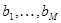. Результатом фильтрации исходного сигнала назовем функцию 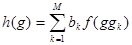. Результат фильтрации оценивается с точки зрения изменения спектра. Имеем : =

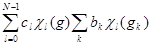
Другими словами, числа

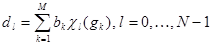(1)

задают передаточную функцию фильтра.