Получим частотную передаточную функцию в виде

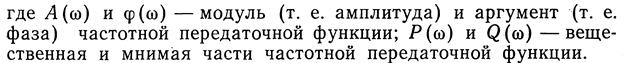
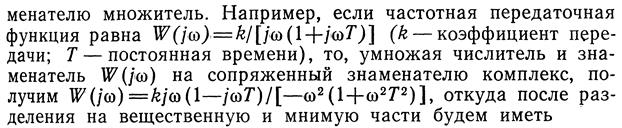
Для наглядного представления частотных свойств динамических звеньев используются так называемые частотные характеристики: во-первых, амплитудная частотная характеристика (АЧХ), которая определяет зависимость амплитуды выходного сигнала от частоты колебаний при постоянстве амплитуды входного сигнала (рис. 2.3, а) ; во-вторых, фазовая частотная характеристика (ФЧХ), показывающая фазовые сдвиги, вносимые звеном на разных частотах (рис. 2.3, б) ; в-третьих, амплитудно-фазовая частотная характеристика '(АФЧХ), которая объединяет амплитудную и фазовую частотные характеристики при использовании их в качестве полярных координат (рис. 2.3, в), Каждая точка АФЧХ соответствует определенному значению частоты ω. Эту характеристику можно построить и в прямоугольной системе координат — в комплексной плоскости. При этом координатами будут показанные на рис. 2.3, в проекции Р и Q вектора А на соответствующие оси.

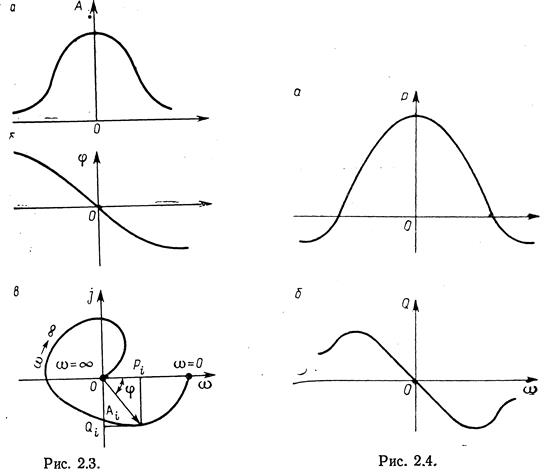
Иногда строятся также вещественная Р() и мнимая Р(со) частотные характеристики (рис. 2.4).

Согласно формулам (2.6) и (2.7) связь между названными частотными характеристиками определяется следующими выражениями:

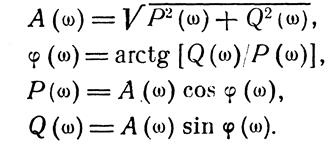
При исследовании САУ амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это даёт возможность очень просто построить логарифмические частотные характеристики (ЛЧХ) даже для сложных устройств. Прологарифмируем выражение частотной передаточной функции (2.6)

Ln W(jω) = ln A(ω)+jφ(ω)

Из этого выражения видно, что член ln A(ω) определяет логарифмическую амплитудную частотную характеристику (ЛАХ), а φ (ω) – логарифмическую фазовую частотную характеристику (ЛФК).

Построение ЛАЧХ и ЛФЧХ систем и звеньев производится в прямоугольной системе координат. Координатные оси представляются в виде шкал, позволяющих произвести разметку осей в определенных единицах измерения. Подготовку системы координат для построения ЛЧХ рассмотрим подробнее.