Основные принципы математического описания динамики объектов и систем.
Известны следующие формы математического описания непрерывных систем: дифференциальными уравнениями, переходными функциями, интегральными и спектральными преобразованиями, а также две формы описания дискретных систем: разностными уравнениями и Z-преобразованием.
Линеаризация уравнений движения.
Работу любой автоматической системы в установившемся и переходном режиме можно описать, использовав дифференциальные уравнения, которые применимы для описания многих явлений природы и, в частности, процессов преобразования и передачи массы или энергии
У реальных элементов и систем связь между входными и выходными величинами, как правило, нелинейная, общее уравнение системы оказывается нелинейным, а аналитическое решение нелинейных уравнений возможно только в редких частных случаях. Поэтому полученные нелинейные уравнения элементов системы необходимо линеаризовать.
Линеаризация уравнений — это замена точного нелинейного уравнения приближенным линейным. Например, алгебраическое нелинейное уравнение
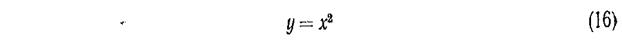
можно заменить приближенным линейным уравнением
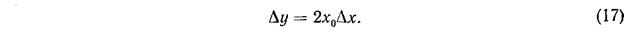
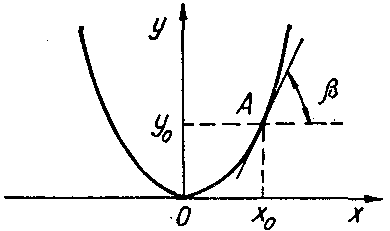
Отметим, что уравнение (17) записано в отклонениях, а не в абсолютных значениях переменных величин.
Основным допущением, на котором базируется линеаризация, является предположение, что независимая переменная изменяется в небольших пределах. Оценим аналитически, какими же должны быть эти пределы. Функцию у в уравнении типа (16) можно разложить в ряд Маклорена в окрестностях точки 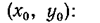
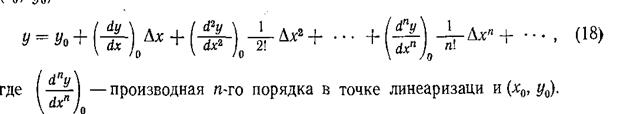 Так как величина
Так как величина  малая, то все слагаемые в формуле (18), кроме первого и второго, будут иметь высшие порядки малости, и ими можно пренебречь. Поскольку величина
малая, то все слагаемые в формуле (18), кроме первого и второго, будут иметь высшие порядки малости, и ими можно пренебречь. Поскольку величина 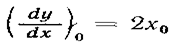 постоянная, то в результате получим линейное уравнение
постоянная, то в результате получим линейное уравнение 
где Д0 = у — у0.
Уравнение (19) является приближенным по отношению к уравнению (18), так как мы пренебрегли слагаемыми высших порядков малости. При этом чем меньше отклонение переменных от их установившихся значений, тем меньше ошибка при замене нелинейного уравнения линейным.
Действительно, из рис. 55 и уравнения (19) следует, что линеаризация уравнения (16) соответствует замене точной кривой у = х2 прямой, касательной в точке линеаризации А,
В тех случаях, когда функция зависит от нескольких переменных, в качестве коэффициентов линейного уравнения будут стоять не простые, а частные производные.

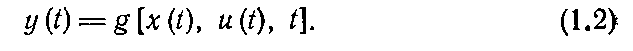
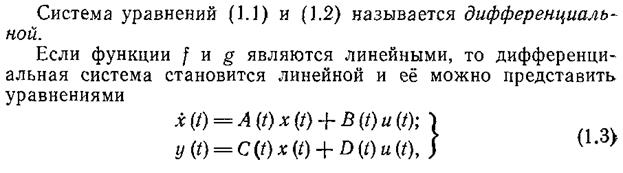

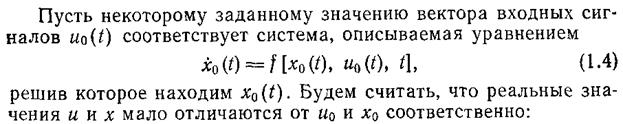
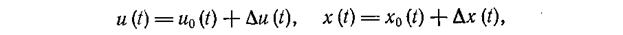

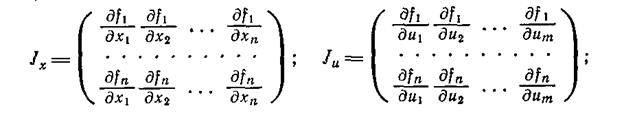
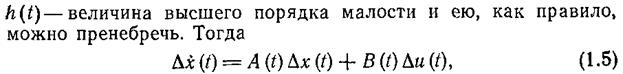

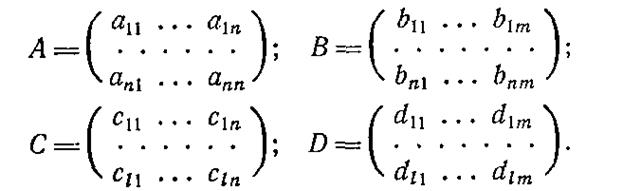
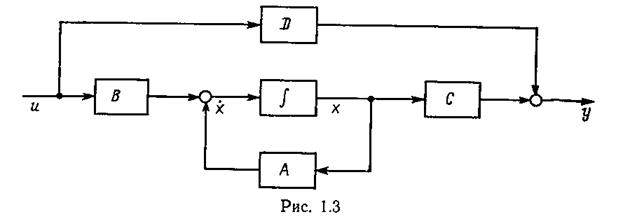

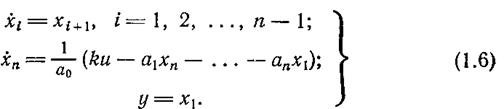
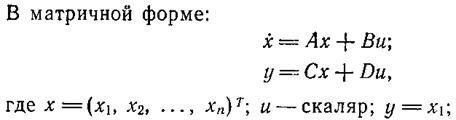

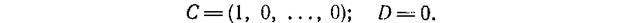
1.3. МОДЕЛИ ТИПА «ВХОД-ВЫХОД»
Математические модели (1.1), (1.2) описывают взаимосвязи между переменными состояния системы, поэтому их называют внутренними. Модели, отражающие зависимость между входными и выходными сигналами системы, называют внешними.
Пусть рассматривается линейная система с одним входом и одним выходом, процессы в которой описываются неоднородным линейным дифференциальным уравнением л-го порядка
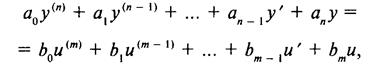 (1.7)
(1.7)
где u(t), u(q)(t) — входной сигнал системы и q = 1, т его производных; y(t), ym(t) — выходной сигнал системы и к = 1, п его производных.
Применив к этому уравнению оператор дифференцирования Коши D = d/d/, получим операторное представление уравнения системы:
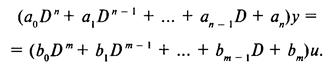
Запишем это представление в иной форме у = B(D)/A(D)u, где обозначено
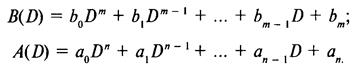
Выражение H(D) — B(D)/A(D) называют операторной передаточной функцией системы, а уравнение
y(t) = H(D)u(t)(1.8)
операторной или внешней моделью системы.
Полином A(D) называют характеристическим многочленом системы, его корни — полюсами или характеристическими числами системы, а корни полинома B(D) — нулями системы.
Представление внешней модели в частотной области позволяет осуществить преобразование Лапласа. Пусть лапласовы преобразования входного и выходного сигналов:
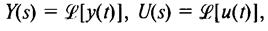
, тогда моделью системы оказывается выражение
Y(s) = H{s)U{s),(1.9)
полученное преобразованием уравнения (1.7)при нулевых начальных условиях.
Выражение H(s) называют передаточной функцией системы.
В теории автоматического управления широко применяется операторная (символическая) форма записи дифференциальных уравнений. В операторной форме дифференциальные уравнения приобретают более простой вид, уменьшается объем записи, а при исследовании САУ во многих случаях сокращаются промежуточные математические преобразования.
Функции независимой переменной (обычно t)- x (t), y (t) в дифференциальных уравнениях заменяются их изображениями по Лапласу.
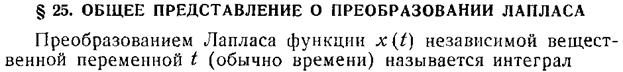
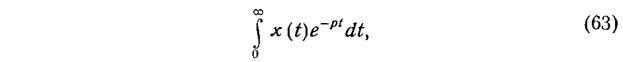

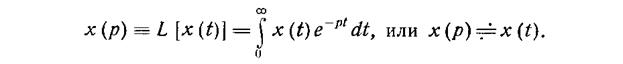
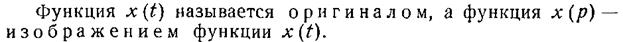
В изображениях по Лапласу операция дифференцирования обозначается следующим образом:
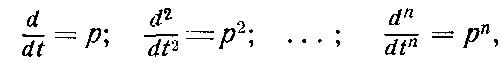
а интегрирования – обратной величиной:


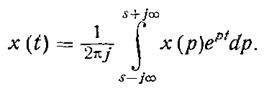
Метод преобразования Лапласа применяется для упрощения решения систем линейных интегро-дифференциальных уравнений с постоянными коэффициентами. Прямое преобразование заданной системы уравнений приводит к более простым уравнениям, которые являются уже не интегро-дифференциальными, а алгебраическими уравнениями. Эта более простая система уравнений решается относительно изображения искомой функции, по которому затем отыскивается искомое решение заданной системы уравнений с помощью обратного преобразования Лапласа. Оба преобразования, прямое и обратное, на практике выполняются с помощью соответствующих таблиц. 

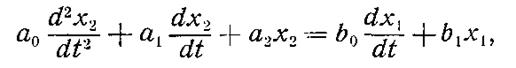
то при нулевых начальных условиях это уравнение в операторной форме запишется так:
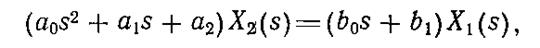
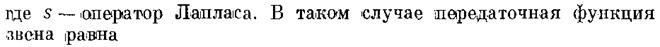
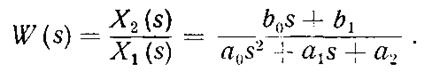
Передаточной функцией (в форме преобразований Лапласа) называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.
При P=0 передаточная функция превращается в коэффициент усиления.
k= 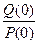 =
= 
Тема V: Описание систем с помощью динамических характеристик и
Дата добавления: 2015-05-16; просмотров: 1328;
