Динамические характеристики линейных звеньев и систем.

Динамической характеристикой системы называют ее реакцию на специальное входное возмущение. Такими специальными — ти­повыми — сигналами являются:

• импульсная дельта-функция {функция Дирака)

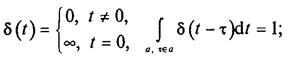
• единичный скачок (функция Хевисайда)

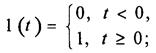
линейное воздействие

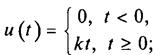
гармоническое воздействие

■5800

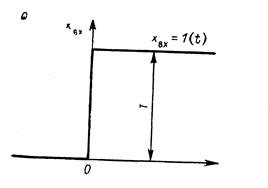
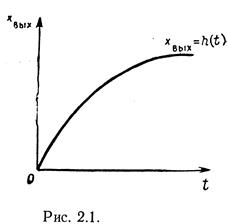
Для оценки динамических свойств звеньев используют временные и частотные характеристики, К временным характеристикам звеньев относятся их переходные функции. Переходная функция звена h(t) определяет его реакцию на единичную ступенчатую функцию x _вх=1(t) (рис. 2.1, а) и характеризует переход звена от одного установившегося состояния к другому (рис. 2.1,6). Выражение функции h(t) можно получить посредством решения дифференциального уравнения, которым описывается динамика данного звена при х_ъх=1(t) и нулевых начальных условиях.

За единичную ступенчатую функцию принимают скачкообразное воздействие с величиной скачка, равной единице при t>0:

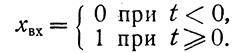
Ступенчатый сигнал — весьма распространенный вид входного воздействия в САУ, например мгновенный поворот задающей оси следящего привода, мгновенное изменение момента нагрузки электропривода и т. д.-

Другим также распространенным видом входного воздействия в САУ является единичная импульсная входная функция или дельта-функция, представляющая собой производную единичной ступенчатой функции:

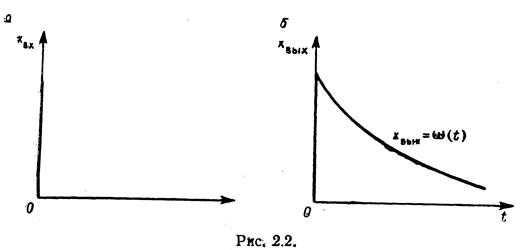
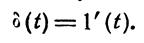
Дельта-функции свойственна тождественность нулю повсюду, кроме точки t=0, в которой она стремится к бесконечности {рис. 2.2, а), т. е.

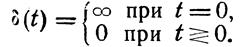
Площадь дельта-функции равна единице, т. е. 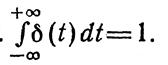. Примером импульсного воздействия может быть кратковременный ток короткого замыкания генератора, который отключается плавкими предохранителями, кратковременный удар нагрузки на валу электродвигателя и т.д.

и наоборот

Учитывая это простое соотношение между переходной и весовой функциями, в дальнейшем будем использовать в основном первую из них, имея в виду, что вторую всегда можно получить из выражения (2.5) .

Через скачок или импульс можно выразить непрерывные сигналы любой формы, представив их в виде суммы скачков или импульсов определённой интенсивности, подаваемых в определённые моменты времени или через равные промежутки времени. Найдя реакцию системы на каждый скачок (импульс) и просуммировав результат, получим реакцию системы на суммарный входной сигнал.

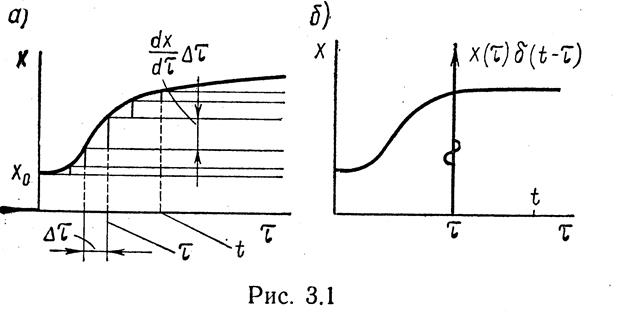
Пусть сигнал представлен некоторой функцией времени х (t).

Используя интеграл Дюамеля в различной форме, данный сигнал можно

представить совокупностью единичных скачков

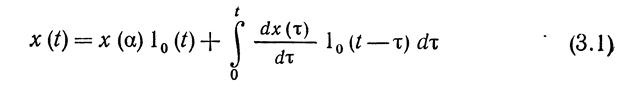
при а -> 0 или совокупностью единичных импульсов

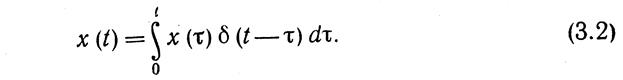
Если входной сигнал задан функцией времени x (t). то сигнал на выходе звена может быть получен с помощью переходной или весовой функции.

Разлагая х (0 на совокупность единичных скачков 1_Р'(t — т) по формуле (ЗЛ) и находя реакцию звена на каждый из скачков, определяем

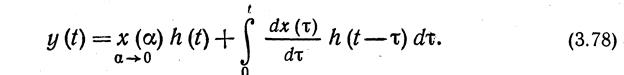
Аналогично, разлагая x (t} на совокупность единичных импульсов б (t — т) по формуле (3,2) и находя реакцию звена на каждый из импульсов, получаем

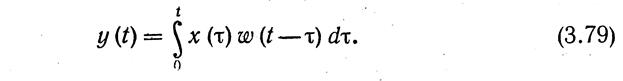
Таким образом, рассмотренные характеристики звеньев дают возможность рассчитать сигнал на выходе звена, если известен сигнал на его входе при нулевых начальных условиях*

Рассмотрим частотную функцию, которая является важнейшей характеристикой динамического звена.