Ось ординат

Эта ось называется осью усиления. При построении ЛАЧХ системы или звена за единицу измерения по оси ординат принимается децибел, при построении ЛФЧХ —градус, при этом применяются следующие масштабы:

I дб = 2 мм, 1 Г = 1 мм. (3.5.6)

С соблюдением этих масштабов и производится разметка оси усиления в указанных единицах измерения.

Децибел — логарифмическая единица для оценки отношения двух величин- Значение какой-либо положительной величины в децибелах численно равно десятичному логарифму этой величины, увеличенному в 20 раз. Например, значение общего коэффициента усиления системы K в децибелах определится по формуле

Кдб = 20 lg K(3.5,7)

Типовая логарифмическая сетка для построения ЛАЧХ и ЛФЧХ с масштабами (3.5.5) и (3.5.6) по осям координат изображена на рис. 3.5.1.

Основные характеристики звеньев и систем.

При синтезе и анализе САУ ее расчленяют на типовые звенья, которые различаются динамическими свойствами.

Характеристики типовых звеньев.

За типовые звенья, по-видимому, целесообразно принять такие, которые могут служить основой для построения любых других звеньев, встречающихся на практике. Обычно за основу принимают звено, обладающее одной степенью свободы. Математические процессы в таком звене описываются дифференциальным уравнением не выше второго порядка

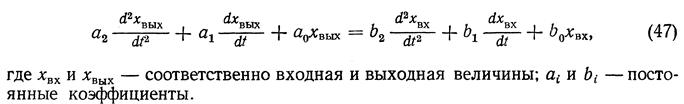
В основу классификации звеньев кладётся вид дифференциального уравнения, которым могут описываться весьма разнообразные свойства как по своей функции, так и по своему конструктивному исполнению.

Если принять это уравнение за исходное, то легко вывести уравнения различных типовых звеньев.

Типовые звенья являются звеньями направленного действия: сигналы передаются звеном в одном направлении — со входа на выход.

Типовые звенья подразделяют на пропорциональные (усилительные), апериодические (инерционные), колебательные, интегрирующие, дифференцирующие и форсирующие. Несколько обособленно в этой классификации стоит запаздывающее звено.

Дифференциальные уравнения и основные характеристики типовых звеньев, рассмотренные далее, приведены в табл. 1.

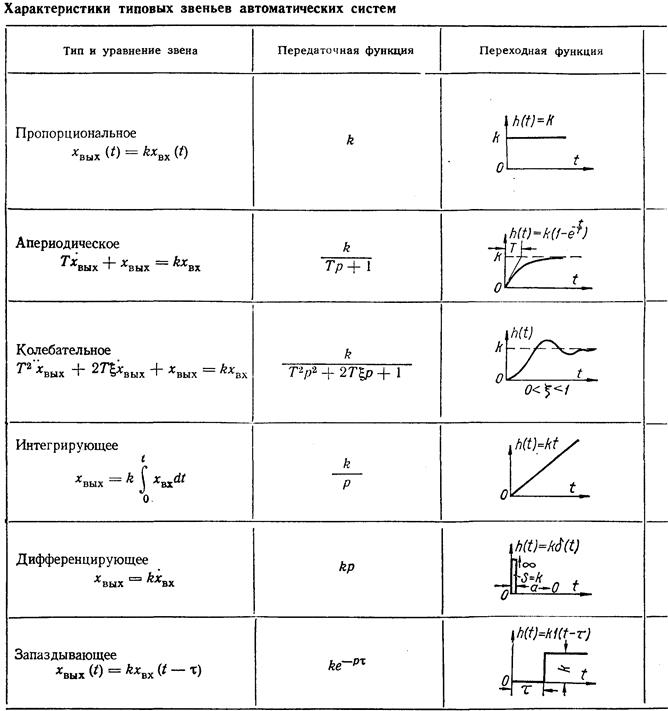
Из рассмотренных типовых звеньев элементарными явля­ются пропорциональное, интегрирующее и дифференцирующее. Все другие звенья можно сформировать из элементарных пу­тем соответствующего соединения их между собой.

Звенья, у которых переходная функция со временем зату­хает, называются устойчивыми. Типовые звенья всегда устой­чивы. Их действие описывается линейными дифференциальны­ми уравнениями с положительными коэффициентами. Исклю­чение составляет интегрирующее звено, которое исходя из усло­вий устойчивости, называют нейтральным. В неустойчивых: звеньях переходный процесс является расходящимся. Действие этих звеньев описывается линейными дифференциальными урав­нениями с отрицательными коэффициентами.

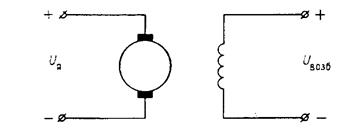
Следует заметить, что в зависимости от сигналов, приняты за входной и выходной, а также от принятых при составлении дифференциальных уравнений допущений один и тот же элемент САУ можно описать разными уравнениями, а значит, отобразить различными типовыми звеньями. Например, если для электродвигателя постоянного тока (рис. 2.14) за входной сигнал принято напряжение на якоре и_я {и_во3(> — напряжение возбуждения двигателя), а за выходной — угол поворота а вы­ходного вала и если такой электродвигатель считать безынер­ционным, то он будет отображен интегрирующим звеном:

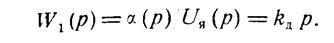
Если для этого же электродвигателя за выходной сигнал при­нять скорость вращения Q = a, то он будет уже представлен безынерционным (пропорциональным) звеном:

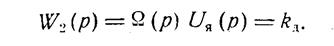
Если же при тех же входных и выходных сигналах учесть инерционность электродвигателя, то он должен быть отобра­жен либо двумя последовательно включенными звеньями — ин­тегрирующим и апериодическим:

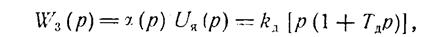
либо одним апериодическим звеном:

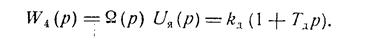
В зависимости от сложности дифференциального уравнения элемента САУ последний может быть представлен одним или несколькими типовыми звеньями, определенным образом соеди­ненными между собой.