Геометрические изображения комплексных чисел
Рассмотрим декартову числовую плоскость.

Изобразим комплексное число с = (a,b) = a+i·b точкой М(a,b). Эту точку М мы будем называть аффиксом комплексного числа с = (a,b) (аффикс – отметка). В дальнейшем эти точки мы будем также обозначать буквой с, и отождествлять комплексные числа с соответствующими точками декартовой плоскости.
Плоскость, точки которой являются изображением комплексных чисел, называется комплексной плоскостью, ее обозначают символами (Z) или (W).
Легко видеть, что действительные числа а = (а,0) изображаются точками оси иксов (oX), поэтому ось абсцисс называется действительной осью.
Мнимые числа с = (a,b) = a+i·b (b ≠ 0) изображаются точками, не лежащими на оси абсцисс. Чисто мнимые числа c = (0,b) = b·i (b ≠ 0) изображаются точками оси ординат, поэтому эту ось в комплексной плоскости называют мнимой осью.
Начало координат (0,0) является изображением комплексного числа 0, поэтому оно называется нулем. Отметим, что комплексные числа Z=x+i·y=(x,y) также изображаются векторами плоскости с проекциями x и y. Начало вектора может быть помещено в любую точку.
Изобразим комплексное число Z = (x,y) = x+i·y вектором, начало которого помещено в нуль.

Длина этого вектора очевидно равна 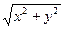 и называется модулем комплексного числа Z и обозначается
и называется модулем комплексного числа Z и обозначается 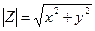 .
.
Угол, который составляет этот вектор с положительным направлением действительной оси, называется аргументом комплексного числа Z и обозначается ArgZ. Этот угол определяется неоднозначно, а с точностью до слагаемых кратных 2π. Отметим, что направление отсчета углов против часовой стрелки принимают за положительное, а по часовой стрелке за отрицательное.
Среди бесконечного множества значений ArgZ есть одно такое, которое содержится в полуинтервале 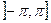 , оно называется главным значением аргумента числа Z и обозначается символом argZ.
, оно называется главным значением аргумента числа Z и обозначается символом argZ.
Очевидно ArgZ = argZ+2πk (к = 0, 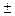 1,
1, 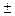 2,…). Легко доказывается, что для комплексных чисел Z = x+y·i
2,…). Легко доказывается, что для комплексных чисел Z = x+y·i
argZ = 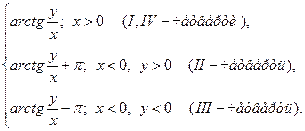
Дата добавления: 2015-06-12; просмотров: 1567;
